题目内容
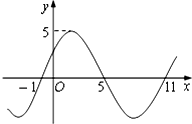 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0≤φ<2π)在R上的部分图象如图所示,则f(2014)=
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0≤φ<2π)在R上的部分图象如图所示,则f(2014)=考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:由最大值可得A,由周期T=2[5-(-1)]=12可求ω,根据f(-1)=0及0≤φ<2π可得φ.
解答:
解:由函数的图象可得A=5,周期T=
=11-(-1)=12,∴ω=
.
再由五点法作图可得
(-1)+φ=0,∴φ=
,故函数f(x)=5sin(
x+
).
故f(2014)=5sin(
+
)=5sin
=5sin(336π-
)=5sin(-
)=-5sin
=-
,
故答案为:-
.
| 2π |
| ω |
| π |
| 6 |
再由五点法作图可得
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
故f(2014)=5sin(
| 2014π |
| 6 |
| π |
| 6 |
| 2015π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 5 |
| 2 |
故答案为:-
| 5 |
| 2 |
点评:本题考查由y=Asin(ωx+φ)的部分图象确定解析式,考查数形结合思想,属中档题.

练习册系列答案
相关题目
小路、小华与小敏三位同学讨论一道数学题,当他们每个人都把自己的解法说出来以后,小路说:“我做错了,”小华说:“小路做对了,”小敏说:“我做错了.”老师看过他们的答案并听了他们以上的陈述之后说:“你们三位同学中只有一人做对了,只有一人说对了.”那么请问:根据老师的回答,谁做对了呢?( )
| A、小路 | B、小华 |
| C、小敏 | D、不能确定 |
若a,b,c为实数,且a<b<0,则下列命题正确的是( )
| A、ac2<bc2 | ||||
B、
| ||||
C、
| ||||
| D、a2>ab>b2 |
函数y=kx+b与函数y=
在同一坐标系中的大致图象正确的是( )
| kb |
| x |
A、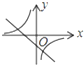 |
B、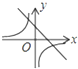 |
C、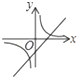 |
D、 |
若曲线C1:x2+y2-8x=0与曲线C2:y(y-mx-m)=0有四个不同交点,则实数m的取值范围是( )
A、(-
| ||||
B、(-
| ||||
C、[-
| ||||
D、(-∞,-
|