题目内容
（1）化简
（a＞0，b＞0）（结果写成分数指数幂形式）；
（2）计算log2
+log212-
log242的值．
a-4b2•
|
（2）计算log2
|
| 1 |
| 2 |
考点：对数的运算性质
专题：函数的性质及应用
分析：（1）利用分数指数幂的运算法则即可得出；
（2）利用对数的运算法则即可得出．
（2）利用对数的运算法则即可得出．
解答：
解：（1）原式=
=
=a-
b
，
（2）原式=
log2
=
log2
=-
．
a-4b2•a
|
a-
|
| 11 |
| 6 |
| 4 |
| 3 |
（2）原式=
| 1 |
| 2 |
| ||
| 42 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评：本题考查了分数指数幂的运算法则、对数的运算法则，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知正项等比数列{an}满足a3•a2n-3=4n（n＞1），则log2a1+log2a3+log2a5+…+log2a2n-1=（ ）
| A、n2 |
| B、（n+1）2 |
| C、n（2n-1） |
| D、（n-1）2 |
若函数f（x）=sin（
-2x）×sin（
+2x），则f（x）的最小正周期是（ ）
| π |
| 4 |
| π |
| 4 |
A、
| ||
| B、π | ||
| C、2π | ||
D、
|
已知集合A={x|-1≤x≤3}，集合B={x|
＜0}，则A∪B=（ ）
| 1 |
| x |
| A、{x|-1＜x＜0} |
| B、{x|-1≤x＜0} |
| C、{x|x＜0} |
| D、{x|x≤3} |
三个数e-
，log0.23，lnπ的大小关系为（ ）
| 2 |
A、log0.23＜e-
| ||
B、log0.23＜lnπ＜e-
| ||
C、e-
| ||
D、log0.23＜lnπ＜e-
|
如图，已知抛物线C：y2=x和⊙M：（x-4）2+y2=1，过抛物线C上一点H（x0，y0）（y0≥1）做两条直线与⊙M相切于A、B两点，分别交抛物线于E、F两点．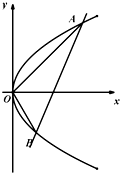
如图，已知抛物线y2=2px（p＞0）上点（2，a）到焦点F的距离为3，直线l：my=x+t（t≠0）交抛物线C于A，B两点，且满足OA⊥OB．圆E是以（-p，p）为圆心，p为直径的圆．