题目内容
已知正项等比数列{an}满足a3•a2n-3=4n(n>1),则log2a1+log2a3+log2a5+…+log2a2n-1=( )
| A、n2 |
| B、(n+1)2 |
| C、n(2n-1) |
| D、(n-1)2 |
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:根据所给的等式a3•a2n-3=4n,可以看出数列中的下标之和为2n时的两项之积是4n,所以对要求的结论先用对数的性质进行整理,把下标和是2n的两项放在一起,再计算对数的结果.
解答:
解:∵a3•a2n-3=4n,
∴log2a1+log2a3+…+log2a2n-1
=log2(a1a2…a2n-1)
=log2(a1a2n-1a3a2n-3…)
=log2(4n)
=n2,
故选A.
∴log2a1+log2a3+…+log2a2n-1
=log2(a1a2…a2n-1)
=log2(a1a2n-1a3a2n-3…)
=log2(4n)
| n |
| 2 |
故选A.
点评:本题考查数列求和,对数的运算性质,使学生系统掌握解等差数列与等比数列综合题的规律,深化数学思想方法在解题实践中的指导作用,灵活地运用数列知识和方法解决数学和实际生活中的有关问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若m+n=1(mn>0),则
+
的最小值为( )
| 1 |
| m |
| 1 |
| n |
| A、1 | B、2 | C、3 | D、4 |
等差数列{an}满足a8>0,a9<0,则n=( )时,{an}前n项和最大.
| A、6 | B、7 | C、8 | D、9 |
已知数列{an}的前n项和Sn=an-1(a是不为0的常数),那么数列{an}( )
| A、一定是等差数列 |
| B、一定是等比数列 |
| C、或者是等差数列或者是等比数列 |
| D、既不是等差数列也不是等比数列 |
已知函数f(x)=3x+x,g(x)=log3x+2,h(x)=log3x+x的零点依次是a,b,c,则a,b,c,的大小关系是( )
| A、a<b<c |
| B、a<c<b |
| C、c<b<a |
| D、b<a<c |
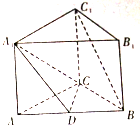 如图,直三棱柱ABC-A
如图,直三棱柱ABC-A