题目内容
下列有关命题的说法,正确的有 .
(1)命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”;
(2)若p∧q为假命题,则p,q均为假命题;
(3)“x=1”是“x2-3x+2=0”的充分不必要条件;
(4)命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,x2+x+1≥0.
(1)命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”;
(2)若p∧q为假命题,则p,q均为假命题;
(3)“x=1”是“x2-3x+2=0”的充分不必要条件;
(4)命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,x2+x+1≥0.
考点:命题的真假判断与应用
专题:简易逻辑
分析:(1)直接写出命题的逆否命题判断(1)的真假;
(2)由复合命题真值表判断(2)的真假;
(3)由充分条件、必要条件的概念判断命题(3)的真假;
(4)写出特称命题的否定判断(4)的真假.
(2)由复合命题真值表判断(2)的真假;
(3)由充分条件、必要条件的概念判断命题(3)的真假;
(4)写出特称命题的否定判断(4)的真假.
解答:
解:对于(1),命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”.
∴命题(1)正确;
对于(2),当p,q均为假命题时p∧q为假命题,
∴若p∧q为假命题,则p,q均为假命题正确.
∴命题(2)正确;
对于(3),由x=1得到x2-3x+2=0,解x2-3x+2=0得x=1或x=2.
∴“x=1”是“x2-3x+2=0”的充分不必要条件.
∴命题(3)正确;
对于(4),命题p:?x∈R,使得x2+x+1<0的否定为¬p:?x∈R,x2+x+1≥0.
∴命题(4)正确.
故答案为:(1)(2)(3)(4).
∴命题(1)正确;
对于(2),当p,q均为假命题时p∧q为假命题,
∴若p∧q为假命题,则p,q均为假命题正确.
∴命题(2)正确;
对于(3),由x=1得到x2-3x+2=0,解x2-3x+2=0得x=1或x=2.
∴“x=1”是“x2-3x+2=0”的充分不必要条件.
∴命题(3)正确;
对于(4),命题p:?x∈R,使得x2+x+1<0的否定为¬p:?x∈R,x2+x+1≥0.
∴命题(4)正确.
故答案为:(1)(2)(3)(4).
点评:本题考查了命题的真假判断与应用,解答的关键是熟练掌握教材中有关基本概念,是基础题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
已知数列{an}满足a1=2,an+1=
,则a2014等于( )
| 1+an |
| 1-an |
| A、2 | ||
B、-
| ||
| C、-3 | ||
D、
|
等差数列的相邻4项分别是a+1,a+3,b,a+b,那么a,b的值依次为( )
| A、2,7 | B、1,6 |
| C、0,5 | D、无法确定 |
 如图,△OAB是等腰三角形,P是底边AB延长线上一点,且PO=3,PA•PB=4,则腰长OA=
如图,△OAB是等腰三角形,P是底边AB延长线上一点,且PO=3,PA•PB=4,则腰长OA=
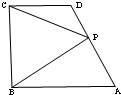 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设