Question

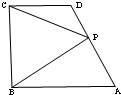如图，在直角梯形ABCD中，AB∥CD，AB⊥BC，AB=2，CD=1，BC=a（a＞0），P为线段AD（含端点）上一个动点，设

AP

=x

AD

，

PB

•

PC

=y，对于函数y=f（x），给出以下四个结论：
①当a=2时，函数f（x）的值域为[1，4]； 
②对任意a＞0，都有f（1）=1成立；
③对任意a＞0，函数f（x）的最大值都等于4；
④存在实数a＞0，使得函数f（x）最小值为0．
其中所有正确结论的序号是

 

．

Answer 1

考点：平面向量数量积的运算

专题：平面向量及应用

分析：如图所示，建立直角坐标系．可得B（0，0），A（2，0），C（0，a），D（1，a）．利用数量积的坐标运算可得f（x）=y=

PB

•

PC

=（1+a²）x²-（4+a²）x+4．x∈[0，1]．通过对a分类讨论，利用二次函数的单调性即可得出．

解答： 解：如图所示，建立直角坐标系．
则B（0，0），A（2，0），C（0，a），D（1，a）．
∵

AP

=x

AD

，
∴

BP

=

BA

+x

AD

=（2，0）+x（-1，a）=（2-x，xa）．
∴

PB

=（x-2，-xa），

PC

=（0，a）-（2-x，xa）=（x-2，a-ax）．
∴y=

PB

•

PC

=（x-2）²-ax（a-ax）
=（1+a²）x²-（4+a²）x+4．x∈[0，1]．
①当a=2时，y=f（x）=5x²-8x+4=5(x-

4

5

)2+

4

5

．
当x=

4

5

时，函数y取得最小值

4

5

；
又f（0）=4，f（1）=1，∴函数f（x）的最大值为4．
因此函数f（x）的值域为：[

4

5

，1]．
②对任意a＞0，都有f（1）=1+a²-（4+a²）+4=1成立，正确；
③对任意a＞0，函数f（x）=(1+a2)[x-

4+a2

2(1+a2)

]2+

8a2-a4

4(1+a2)

．
当a≥

2

时，0＜

4+a2

2(1+a2)

≤1，而f（0）=4，f（1）=1，因此函数f（x）的最大值等于4；
当0＜a＜

2

时，

4+a2

2(1+a2)

＞1，∴函数f（x）在[0，1]内单调递减，而f（0）=4取得最大值．
综上可知：对任意a＞0，函数f（x）的最大值都等于4．
④由③可知：当a≥

2

时，当x=

4+a2

2(1+a2)

时，函数f（x）取得最小值

8a2-a4

4(1+a2)

，令

8a2-a4

4(1+a2)

=0，
解得a=2

2

，当a=2

2

时，使得函数f（x）最小值为0．
当0＜a＜

2

时，

4+a2

2(1+a2)

＞1，∴函数f（x）在[0，1]内单调递减，而f（1）=1取得最小值．
综上可知：存在实数a=2

2

＞0，使得函数f（x）最小值为0．
综上可知：只有②③④正确．
故答案为：②③④．

点评：本题综合考查了向量的坐标运算、数量积的运算性质、二次函数的单调性、分类讨论的思想方法等基础知识与基本技能方法，考查了推理能力和计算能力，属于难题．