题目内容
已知椭圆C:
+
-1(a>b>0)的左、右顶点分别为A1,A2,P为椭圆上异于A1,A2的点,|A1A2|=6,PA1和PA2的斜率之积为-
.
(1)求椭圆C的标准方程;
(2)设O为椭圆中心,M,N是椭圆上的异于顶点的两个动点,求△OMN面积的最大值,并求面积取得最大值时,OM与ON的斜率之积是多少?
| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 9 |
(1)求椭圆C的标准方程;
(2)设O为椭圆中心,M,N是椭圆上的异于顶点的两个动点,求△OMN面积的最大值,并求面积取得最大值时,OM与ON的斜率之积是多少?
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(1)由已知得A1(-3,0),A2(3,0),利用斜率计算公式可得kPA1•kPA2=
=-
,由于P(x0,y0)在椭圆C:
+
=1(a>b>0)上,可得
=-
,又2a=6,解出即可.
(2)设M(x1,y1),N(x2,y2).利用三角形面积计算公式与柯西不等式即可得出.
| y02 |
| x02-9 |
| 4 |
| 9 |
| x2 |
| a2 |
| y2 |
| b2 |
| y02 |
| x02-a2 |
| b2 |
| a2 |
(2)设M(x1,y1),N(x2,y2).利用三角形面积计算公式与柯西不等式即可得出.
解答:
解:(1)由已知得A1(-3,0),A2(3,0),
设P(x0,y0),则kPA1=
,kPA2=
,
∵PA1和PA2的斜率之积为-
,
∴kPA1•kPA2=
•
=
=-
,
∵P(x0,y0)在椭圆C:
+
=1(a>b>0)上,
∴
+
=1,∴
=-
,
又2a=6.
∴a2=9,b2=4,
∴椭圆C的标准方程为
+
=1.
(2)设M(x1,y1),N(x2,y2).
∴S△MON=
|x1y2-x2y1|=
|
•
+
•
|≤3
=3,
∴△MON的面积的最大值为3.
当且仅当:
=-
时,取等号,此时kOM•kON=-
.
设P(x0,y0),则kPA1=
| y0 |
| x0+3 |
| y0 |
| x0-3 |
∵PA1和PA2的斜率之积为-
| 4 |
| 9 |
∴kPA1•kPA2=
| y0 |
| x0+3 |
| y0 |
| x0-3 |
| y02 |
| x02-9 |
| 4 |
| 9 |
∵P(x0,y0)在椭圆C:
| x2 |
| a2 |
| y2 |
| b2 |
∴
| x02 |
| a2 |
| y02 |
| b2 |
| y02 |
| x02-a2 |
| b2 |
| a2 |
又2a=6.
∴a2=9,b2=4,
∴椭圆C的标准方程为
| x2 |
| 9 |
| y2 |
| 4 |
(2)设M(x1,y1),N(x2,y2).
∴S△MON=
| 1 |
| 2 |
| 6 |
| 2 |
| x1 |
| 3 |
| y2 |
| 2 |
| -x2 |
| 3 |
| y1 |
| 2 |
[(
|
∴△MON的面积的最大值为3.
当且仅当:
| y1y2 |
| x1x2 |
| 4 |
| 9 |
| 4 |
| 9 |
点评:本题考查了椭圆的标准方程及其性质、斜率计算公式、柯西不等式、三角形的面积计算公式,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
设x,y满足约束条件
,若z=|
|的最小值为3,则a的值为( )
|
| x+2y+3 |
| x-1 |
| A、-1 | B、1 | C、-2 | D、2 |
 已知函数f(x)=(2x+1)ln(2x+1)-a(2x+1)2-x(a>0).
已知函数f(x)=(2x+1)ln(2x+1)-a(2x+1)2-x(a>0).
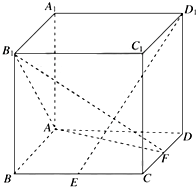 如图,正方体ABCD-A1B1C1D1中,E是棱BC的中点,点F是棱CD上的动点.
如图,正方体ABCD-A1B1C1D1中,E是棱BC的中点,点F是棱CD上的动点.