题目内容
 已知函数f(x)=(2x+1)ln(2x+1)-a(2x+1)2-x(a>0).
已知函数f(x)=(2x+1)ln(2x+1)-a(2x+1)2-x(a>0).(1)若函数f(x)在x=0处取极值,求a的值;
(2)如图,设直线x=-
| 1 |
| 2 |
(3)比较32×43×54×…×20142013与23×34×45×…×20132014的大小,并说明理由.
考点:利用导数研究函数的极值,对数函数的图像与性质
专题:计算题,函数的性质及应用,导数的综合应用
分析:(1)求导f′(x)=2ln(2x+1)-4a(2x+1)+1,从而由题意可得f′(0)=-4a+1=0,从而求a并检验;
(2)函数的定义域为(-
,+∞),由题意可得f(x)<-x,从而可得a>
,令h(x)=
,化为函数的最值问题;
(3)由函数h(x)=
在(
,+∞)上单调递减可得函数P(x)=
在(e,+∞)上单调递减,从而可推出当x∈(e,+∞)时,(x-1)x>x(x-1),从而判断大小关系.
(2)函数的定义域为(-
| 1 |
| 2 |
| ln(2x+1) |
| 2x+1 |
| ln(2x+1) |
| 2x+1 |
(3)由函数h(x)=
| ln(2x+1) |
| 2x+1 |
| e-1 |
| 2 |
| lnx |
| x |
解答:
解:(1)f(x)=(2x+1)ln(2x+1)2-a(2x+1)2-x(a>0),
f′(x)=2ln(2x+1)-4a(2x+1)+1;
∵f(x)在x=0处取极值,
∴f′(0)=-4a+1=0.
∴a=
(经检验a=
符合题意).
(2)因为函数的定义域为(-
,+∞),
且当x=0时,f(0)=-a<0.
又直线y=-x恰好通过原点,
所以函数y=f(x)的图象应位于区域Ⅳ内,
于是可得f(x)<-x,
即(2x+1)ln(2x+1)2-a(2x+1)2-x<-x.
∵2x+1>0,
∴a>
.
令h(x)=
,
∴h′(x)=
,
令h′(x)=0,得x=
.
∵x>-
,
∴x∈(-
,
)时,h′(x)>0,h(x)单调递增,
x∈(
,+∞)时,h′(x)<0,h(x)单调递减.
∴hmax(x)=h(
)=
.
∴a的取值范围是a>
.
(3):由(2)知,函数h(x)=
在(
,+∞)上单调递减,
函数P(x)=
在(e,+∞)上单调递减.
∴
>
,
∴xln(x-1)>(x-1)lnx;
∴ln(x-1)x>lnx(x-1),
即当x∈(e,+∞)时,(x-1)x>x(x-1),
∴令x=4,5,…,2011,
则34>43,45>54,…,20112012>20122011;
又∵23×34>32×43;
∴32×43×54×…×20142013<23×34×45×…×20132014.
f′(x)=2ln(2x+1)-4a(2x+1)+1;
∵f(x)在x=0处取极值,
∴f′(0)=-4a+1=0.
∴a=
| 1 |
| 4 |
| 1 |
| 4 |
(2)因为函数的定义域为(-
| 1 |
| 2 |
且当x=0时,f(0)=-a<0.
又直线y=-x恰好通过原点,
所以函数y=f(x)的图象应位于区域Ⅳ内,
于是可得f(x)<-x,
即(2x+1)ln(2x+1)2-a(2x+1)2-x<-x.
∵2x+1>0,
∴a>
| ln(2x+1) |
| 2x+1 |
令h(x)=
| ln(2x+1) |
| 2x+1 |
∴h′(x)=
| 2-2ln(2x+1) |
| (2x+1)2 |
令h′(x)=0,得x=
| e-1 |
| 2 |
∵x>-
| 1 |
| 2 |
∴x∈(-
| 1 |
| 2 |
| e-1 |
| 2 |
x∈(
| e-1 |
| 2 |
∴hmax(x)=h(
| e-1 |
| 2 |
| 1 |
| e |
∴a的取值范围是a>
| 1 |
| e |
(3):由(2)知,函数h(x)=
| ln(2x+1) |
| 2x+1 |
| e-1 |
| 2 |
函数P(x)=
| lnx |
| x |
∴
| ln(x-1) |
| x-1 |
| lnx |
| x |
∴xln(x-1)>(x-1)lnx;
∴ln(x-1)x>lnx(x-1),
即当x∈(e,+∞)时,(x-1)x>x(x-1),
∴令x=4,5,…,2011,
则34>43,45>54,…,20112012>20122011;
又∵23×34>32×43;
∴32×43×54×…×20142013<23×34×45×…×20132014.
点评:本题考查了导数的综合应用及恒成立问题的处理方法,同时考查了构造函数比较大小的方法,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知集合A={x|y=
},B={y|y=ex2,x∈(-1,
]},则A∩B=( )
|
| 2 |
| A、[e,4] |
| B、[e,e2] |
| C、[1,2] |
| D、(1,4] |
从4名男生和2名女生中任选3人参加演讲比赛,所选3人中至少有1名女生的概率为
,那么所选3人都是男生的概率为( )
| 4 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
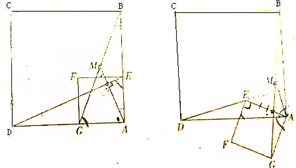 图1和图2中的四边形ABCD和AEFG都是正方形.
图1和图2中的四边形ABCD和AEFG都是正方形.