题目内容
求过点M（1，-4）与圆（x-1）2+（y+3）2=1相切的直线方程．
考点：圆的切线方程
专题：直线与圆
分析：判断点M与圆的关系，即可得到结论．
解答：
解：∵点M的坐标满足圆的方程，
∴点M在圆上，
圆（x-1）2+（y+3）2=1，圆心坐标是C（1，-3），半径r=1，
则CM的斜率不存在，即切线斜率k=0．
此时直线方程为y=4．
所求的切线方程为y=4．
∴点M在圆上，
圆（x-1）2+（y+3）2=1，圆心坐标是C（1，-3），半径r=1，
则CM的斜率不存在，即切线斜率k=0．
此时直线方程为y=4．
所求的切线方程为y=4．
点评：本题主要考查了直线与圆相切的性质的应用，判断点M在圆上是解决本题的关键．
练习册系列答案
口算题天天练系列答案
相关题目
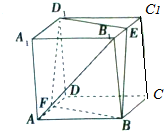如图所示，E，F分别为正方体ABCD-A1B1C1D1的棱B1C1和AD的中点，求证：