题目内容
已知函数f(x)=
.若关于x的不等式f(x)<f(ax+1)的解集中有且仅有2个整数,则实数a的取值范围为 .
|
考点:根的存在性及根的个数判断
专题:
分析:由题意先将不等式f(x)<f(ax+1)化简,将问题转化为含绝对值符号的一次不等式的解的问题来处理,则借助于数形结合的思想容易解决问题.
解答:
 解:由解析式得:函数f(x)的图象关于直线x=1对称,且当x>1时,函数递增,
解:由解析式得:函数f(x)的图象关于直线x=1对称,且当x>1时,函数递增,
所以f(x)<f(ax+1)可化为:|x-1|<|ax+1-1|,
即|x-1|<||ax|,由于该解集中只有两个整数,所以该集合应该是两边夹的形式,
根据函数y=|x-1|,y=|ax|的图象可知,0<|a|<1,
解得
<x<
,记该不等式解集为A,
显然整数1属于A,则有另一个整数2∈A,所以2<
≤3,
解得a∈[-
,-
)∪(
,
].
故答案为a∈[-
,-
)∪(
,
].
 解:由解析式得:函数f(x)的图象关于直线x=1对称,且当x>1时,函数递增,
解:由解析式得:函数f(x)的图象关于直线x=1对称,且当x>1时,函数递增,所以f(x)<f(ax+1)可化为:|x-1|<|ax+1-1|,
即|x-1|<||ax|,由于该解集中只有两个整数,所以该集合应该是两边夹的形式,
根据函数y=|x-1|,y=|ax|的图象可知,0<|a|<1,
解得
| 1 |
| 1+|a| |
| 1 |
| 1-|a| |
显然整数1属于A,则有另一个整数2∈A,所以2<
| 1 |
| 1-|a| |
解得a∈[-
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
故答案为a∈[-
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
点评:本题考查了利用数形结合思想解决不等式的问题,关键是能根据题意将原不等式进行化简,然后求解.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
已知a,b,c∈R,且a<b,则( )
| A、a3>b3 | ||||
| B、a2<b2 | ||||
C、
| ||||
| D、ac2≤bc2 |
已知集合A={x|x=a+b
,a,b∈Z},x1,x2∈A,下列结论不正确的是( )
| 3 |
| A、x1+x2∈A | ||
| B、x1-x2∈A | ||
| C、x1x2∈A | ||
D、当x2≠0时,
|
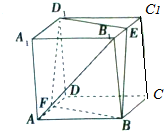 如图所示,E,F分别为正方体ABCD-A1B1C1D1的棱B1C1和AD的中点,求证:
如图所示,E,F分别为正方体ABCD-A1B1C1D1的棱B1C1和AD的中点,求证: