题目内容
设x,y满足约束条件
,若z=|
|的最小值为3,则a的值为( )
|
| x+2y+3 |
| x-1 |
| A、-1 | B、1 | C、-2 | D、2 |
考点:简单线性规划的应用
专题:计算题,作图题,不等式的解法及应用
分析:首先做出平面区域,再化简z=|
|=|1+2
|,而
的几何意义是阴影内的点与点A(1,-2)的连线的斜率,从而求最小值为3,从而得a.
| x+2y+3 |
| x-1 |
| y+2 |
| x-1 |
| y+2 |
| x-1 |
解答:
解:由题意作出其平面区域,

z=|
|=|1+2
|,
的几何意义是阴影内的点与点A(1,-2)的连线的斜率,
令y=0解得,x=3a;故B(3a,0)
故1+2
=3;
故3a-1=2;
故a=1;
故选B.

z=|
| x+2y+3 |
| x-1 |
| y+2 |
| x-1 |
| y+2 |
| x-1 |
令y=0解得,x=3a;故B(3a,0)
故1+2
| 0+2 |
| 3a-1 |
故3a-1=2;
故a=1;
故选B.
点评:本题考查了简单线性规划,作图要细致认真,用到了表达式的几何意义的转化,属于中档题.

练习册系列答案
相关题目
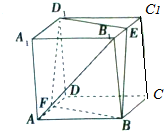 如图所示,E,F分别为正方体ABCD-A1B1C1D1的棱B1C1和AD的中点,求证:
如图所示,E,F分别为正方体ABCD-A1B1C1D1的棱B1C1和AD的中点,求证: