题目内容
在△ABC中,已知,AB=5,AC=3,BC=6,求△ABC的面积.

考点:正弦定理
专题:计算题,解三角形
分析:运用余弦定理,求得cosB,再求sinB,再由三角形的面积公式S=
AB•BC•sinB,即可计算得到.
| 1 |
| 2 |
解答:
解:在三角形ABC中,
cosB=
=
,
则sinB=
=
=
,
则三角形ABC的面积为S=
AB•BC•sinB
=
×5×6×
=2
.
cosB=
| 52+62-32 |
| 2×5×6 |
| 13 |
| 15 |
则sinB=
| 1-cos2B |
1-(
|
2
| ||
| 15 |
则三角形ABC的面积为S=
| 1 |
| 2 |
=
| 1 |
| 2 |
2
| ||
| 15 |
| 14 |
点评:本题考查三角形的余弦定理和面积公式的运用,考查运算能力,属于基础题.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
已知a,b,c∈R,且a<b,则( )
| A、a3>b3 | ||||
| B、a2<b2 | ||||
C、
| ||||
| D、ac2≤bc2 |
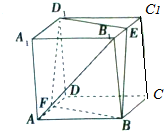 如图所示,E,F分别为正方体ABCD-A1B1C1D1的棱B1C1和AD的中点,求证:
如图所示,E,F分别为正方体ABCD-A1B1C1D1的棱B1C1和AD的中点,求证: