题目内容
2.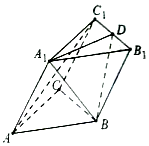 如图,在三棱柱ABC-A1B1C1中,侧面A1ABB1是菱形,侧面C1CBB1是矩形.
如图,在三棱柱ABC-A1B1C1中,侧面A1ABB1是菱形,侧面C1CBB1是矩形.(1)D是棱B1C1上一点,AC1∥平面A1BD,求证:D为B1C1的中点;
(2)若A1B⊥AC1,求证:平面A1ABB1⊥平面C1CBB1.
分析 (1)连结AB1交A1B于E,连结DE,由AC1∥平面A1BD可得AC1∥DE,由E为AB1的中点即可得出D是B1C1的中点;
(2)证明A1B⊥平面AB1C1,得出A1B⊥B1C1,再结合B1C1⊥BB1得出B1C1⊥平面A1ABB1,于是平面A1ABB1⊥平面C1CBB1.
解答 证明:(1)连结AB1交A1B于E,连结DE.
∵AC1∥平面A1BD,AC1?平面AB1C1,平面AB1C1∩平面A1BD=DE,
∴AC1∥DE,
∵侧面A1ABB1是菱形,∴E是AB1的中点,
∴D是B1C1的中点.
(2)∵侧面A1ABB1是菱形,∴AB1⊥A1B,
又A1B⊥AC1,AB1∩AC1=A,AB1?平面AB1C1,AC1?平面AB1C1,
∴A1B⊥平面AB1C1,又B1C1?平面AB1C1,
∴A1B⊥B1C1,
∵侧面C1CBB1是矩形,∴B1C1⊥BB1,
又BB1∩A1B=B,BB1?平面A1ABB1,A1B?平面A1ABB1,
∴B1C1⊥平面A1ABB1.
∵B1C1?平面C1CBB1,
∴平面A1ABB1⊥平面C1CBB1.
点评 本题考查了线面平行的性质,面面垂直的判定,属于中档题.

练习册系列答案
相关题目
12.某几何体的三视图如图所示,则该几何体的体积是( )
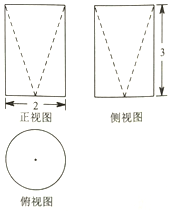

| A. | π | B. | 2π | C. | 3π | D. | 8π |
7.若$cos2α=\frac{7}{25}$,α是第三象限的角,则$sin(α-\frac{π}{4})$=( )
| A. | $-\frac{{7\sqrt{2}}}{10}$ | B. | $-\frac{{\sqrt{2}}}{10}$ | C. | $\frac{{7\sqrt{2}}}{10}$ | D. | $\frac{{\sqrt{2}}}{10}$ |
11.函数y=ln|x|•sinx的图象为( )
| A. |  | B. |  | C. |  | D. |  |
12.若曲线$y=alnx+\frac{1}{2}{x^2}+2x$的切线斜率都是正数,则实数的取值范围是( )
| A. | (1,+∞) | B. | [1,+∞) | C. | (0,+∞) | D. | [0,+∞) |
 如图,已知多面体EABCDF的底面是ABCD边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=$\frac{1}{2}$EA=1.
如图,已知多面体EABCDF的底面是ABCD边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=$\frac{1}{2}$EA=1.