题目内容
12.若曲线$y=alnx+\frac{1}{2}{x^2}+2x$的切线斜率都是正数,则实数的取值范围是( )| A. | (1,+∞) | B. | [1,+∞) | C. | (0,+∞) | D. | [0,+∞) |
分析 求出导函数,利用已知条件列出不等式,求解即可.
解答 解:曲线$y=alnx+\frac{1}{2}{x^2}+2x$,x>0,
可得y′=$\frac{a}{x}$+x+2,由题意可得:$\frac{a}{x}$+x+2>0恒成立,
即a>-x2-2x,
y=-x2-2x,开口向下,x=-1是对称轴,x>0时,函数是减函数,
可得a≥0.
故选:D.
点评 本题考查函数的导数的应用,二次函数的性质的应用,考查计算能力.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
20.已知函数f(x)=sin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的零点构成一个公差为$\frac{π}{2}$的等差数列,$f(0)=-\frac{{\sqrt{3}}}{2}$,则f(x)的一个单调递增区间是( )
| A. | $(-\frac{5π}{12},\frac{π}{12})$ | B. | $(-\frac{π}{6},\frac{π}{3})$ | C. | $(-\frac{π}{12},\frac{5π}{12})$ | D. | $(\frac{π}{12},\frac{7π}{12})$ |
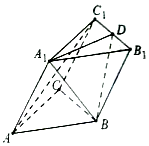 如图,在三棱柱ABC-A1B1C1中,侧面A1ABB1是菱形,侧面C1CBB1是矩形.
如图,在三棱柱ABC-A1B1C1中,侧面A1ABB1是菱形,侧面C1CBB1是矩形.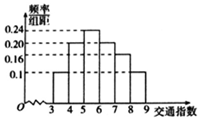 随着社会发展,广州市在一天的上下班时段经常会出现堵车严重的现象.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别;T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10)严重拥堵.早高峰时段(T≥3),从广州市交通指挥中心随机选取了50个交通路段进行调查,依据交通指数数据绘制的直方图如图所示:
随着社会发展,广州市在一天的上下班时段经常会出现堵车严重的现象.交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别;T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10)严重拥堵.早高峰时段(T≥3),从广州市交通指挥中心随机选取了50个交通路段进行调查,依据交通指数数据绘制的直方图如图所示: