题目内容
14. 如图,已知多面体EABCDF的底面是ABCD边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=$\frac{1}{2}$EA=1.
如图,已知多面体EABCDF的底面是ABCD边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=$\frac{1}{2}$EA=1.(Ⅰ)记线段BC的中点为K,在平面ABCD内过点K作一条直线KM,使得KM∥平面ECF,并给予证明.
(Ⅱ)求点B到平面ECF的距离.
分析 (I)取线段CD的中点M,连接KM,直线KM即为所求.借助于KM∥BD∥FG给出证明;
(II)利用VE-DCF=VD-EFC=VA-FDC求出D到平面EFC的距离即可.
解答 解:(Ⅰ)取线段CD的中点M,
连接KM,直线KM即为所求.
证明如下:
取EC中点G,连接FG,连接AC交BD于O.
则OG为△EAC的中位线.
∴OG$\stackrel{∥}{=}$$\frac{1}{2}$EA,又FD$\stackrel{∥}{=}$$\frac{1}{2}$FA,
∴OG$\stackrel{∥}{=}$FD,
∴四边形FGOD为平行四边形,∴FG∥OD.
∵K,M分别为BC,CD的中点,
∴KM∥OD,∴KM∥FG.
∵FG?平面EFC,KM?平面EFC,
∴KM∥平面EFC.
(Ⅱ)由(Ⅰ)知,BD∥FG,又BD?平面EFC,FG?平面EFC,
∴BD∥平面EFC,
∴B到平面EFC的距离等于D到平面EFC的距离,设为h.
∵EA⊥平面ABCD,AD?平面ABCD,
∴EA⊥AD,又FD∥EA,
∴FD⊥AD,
又∵AD⊥CD,CD∩FD=D,
∴AD⊥平面DCF.
∴VE-DCF=VA-DCF=$\frac{1}{3}×\frac{1}{2}×2×1×2$=$\frac{2}{3}$,
在△ECF中,∵EF=FC=$\sqrt{5}$,∴FG⊥EC,
又FG=OD=$\frac{1}{2}$BD=$\sqrt{2}$,EC=$\sqrt{E{A}^{2}+A{C}^{2}}$=2$\sqrt{3}$,∴S△EFC=$\frac{1}{2}×2\sqrt{3}×\sqrt{2}$=$\sqrt{6}$.
∴VD-EFC=$\frac{1}{3}×\sqrt{6}×h$,
∵VE-DCF=VD-EFC,∴$\frac{\sqrt{6}h}{3}$=$\frac{2}{3}$,
解得h=$\frac{\sqrt{6}}{3}$.
∴B到平面EFC的距离为$\frac{\sqrt{6}}{3}$.
点评 本题考查了线面平行的判定,体积与空间距离的计算,属于中档题.

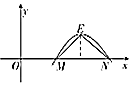 已知奇函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的导函数的部分图象如图所示,E是最高点,且△MNE是边长为1的正三角形,那么$f({\frac{1}{3}})$=( )
已知奇函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的导函数的部分图象如图所示,E是最高点,且△MNE是边长为1的正三角形,那么$f({\frac{1}{3}})$=( )| A. | $-\frac{{\sqrt{3}}}{2π}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $-\frac{3}{4π}$ |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}}{5}$ |
| A. | 若x>0,则x>sinx恒成立 | |
| B. | 命题“若x-sinx=0,则x=0”的否命题为“若x-sinx≠0,则x≠0” | |
| C. | “命题p∧q为真”是“命题p∨q为真”的充分不必要条件 | |
| D. | 命题“?x∈R,x-lnx>0”的否定是“?x0∈R,x0-lnx0<0” |
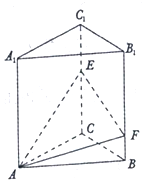 如图,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1,BB1上的点,且EC=2FB.
如图,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1,BB1上的点,且EC=2FB.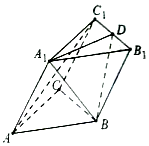 如图,在三棱柱ABC-A1B1C1中,侧面A1ABB1是菱形,侧面C1CBB1是矩形.
如图,在三棱柱ABC-A1B1C1中,侧面A1ABB1是菱形,侧面C1CBB1是矩形.