题目内容
5.一个几何体的三视图如图所示,则该几何体的体积等于( )
| A. | 72 | B. | 48 | C. | 24 | D. | 16 |
分析 如图所示,该几何体为四棱锥P-ABCD.其中底面ABCD是直角梯形,CD$\underset{∥}{=}$$\frac{1}{2}$AB,AB⊥AD,
PA⊥底面ABCD.
解答 解:如图所示,该几何体为四棱锥P-ABCD.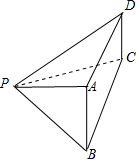
其中底面ABCD是直角梯形,CD$\underset{∥}{=}$$\frac{1}{2}$AB,AB⊥AD,PA⊥底面ABCD.
∴该几何体的体积V=$\frac{1}{3}×PA×{S}_{梯形ABCD}$
=$\frac{1}{3}×$4×$\frac{2+4}{2}×6$=24.
故选:C.
点评 本题考查了四棱锥的三视图、体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
16.已知一个几何体的三视图如图所示,则该几何体的体积为( )


| A. | 2π | B. | $\frac{3π}{2}$ | C. | $\frac{4π}{3}$ | D. | $\frac{7π}{6}$ |
13.已知命题p:已知两条直线l1:x+ay+1=0,l2:(a-2)x+3y+1=0,则a=-1是l1∥l2的充分不必要条件;命题q:“?x∈(0,1),x2-x<0”的否定为“?x0∈(0,1),x02-x0≥0”,则下列命题为真命题的是( )
| A. | p∧(?q) | B. | (?p)∧q | C. | (?p)∧(?q) | D. | p∧q |
10.在区间[0,6]上随机取一实数x,则该实数x满足不等式1≤log2x≤2的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
17.复数$\frac{1}{2+i}$的虚部是( )
| A. | -$\frac{1}{5}$ | B. | -$\frac{1}{5}$i | C. | $\frac{1}{5}$ | D. | $\frac{1}{5}$i |
14.复数z=$\frac{-3+i}{1-i}$的共轭复数为( )
| A. | -1-i | B. | 1-i | C. | -2-i | D. | -2+i |
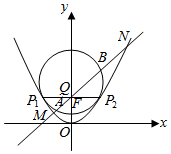 如图,抛物线C:x2=2py(p>0)的准线为y=-1,取过焦点F且平行于x轴的直线与抛物线交于不同的两点P1,P2,过P1,P2作圆心为Q的圆,使抛物线上其余点均在圆外,且∠P1QP2=90°.
如图,抛物线C:x2=2py(p>0)的准线为y=-1,取过焦点F且平行于x轴的直线与抛物线交于不同的两点P1,P2,过P1,P2作圆心为Q的圆,使抛物线上其余点均在圆外,且∠P1QP2=90°.