题目内容
17．复数$\frac{1}{2+i}$的虚部是（ ）| A． | -$\frac{1}{5}$ | B． | -$\frac{1}{5}$i | C． | $\frac{1}{5}$ | D． | $\frac{1}{5}$i |
分析 利用复数的代数形式的乘除运算法则及复数的定义直接求解．
解答 解：复数$\frac{1}{2+i}$=$\frac{2-i}{（2+i）（2-i）}$=$\frac{2-i}{4-{i}^{2}}$=$\frac{2}{5}$-$\frac{1}{5}i$，
∴复数$\frac{1}{2+i}$的虚部为-$\frac{1}{5}$．
故选：A．
点评 本题考查复数的虚部的求法，涉及到复数的代数形式的乘除运算法则、复数的定义等基础知识，考查推理论证能力、运算求解能力，是基础题．
练习册系列答案
相关题目
8．运行如图所示的程序，若输出y的值为1，则输入x的值为（ ）
| A． | 0 | B． | 0或-1 | C． | ±1 | D． | 1 |
5．一个几何体的三视图如图所示，则该几何体的体积等于（ ）
| A． | 72 | B． | 48 | C． | 24 | D． | 16 |
12．已知函数f（x）=$\frac{{{{（x+1）}^2}+asinx}}{{{x^2}+1}}$+1（a∈R），f（ln（log25））=5，则f（ln（log52））=（ ）
| A． | -5 | B． | -1 | C． | 3 | D． | 4 |
9．复数z=$\frac{-4+i}{-i}$的共轭复数是（ ）
| A． | -1+4i | B． | -1-4i | C． | 1+4i | D． | 1-4i |
6．设集合A={x|-a＜x＜a}，其中a＞0，命题p：1∈A，命题q：2∈A，若p∨q为真命题，p∧q为假命题，则a的取值范围是（ ）
| A． | 0＜a＜1或a＞2 | B． | 0＜a＜1或a≥2 | C． | 1＜a≤2 | D． | 1≤a≤2 |
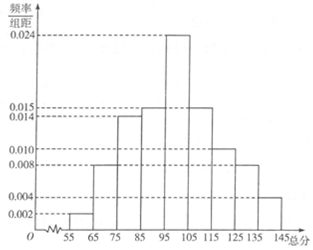某省组织了一次高考模拟考试，该省教育部门抽取了1000名考生的数学考试成绩，并绘制成频率分布直方图如图所示．