题目内容
15.已知数列{an}满足an+1=$\sqrt{2}{a_n},{a_3}$=2,它的前n项和Sn,求$(\sqrt{2}+1){a_{31}}-{S_{30}}$的值.分析 数列{an}满足an+1=$\sqrt{2}$an,可得:数列{an}是等比数列,公比为$\sqrt{2}$.由a3=2,可得${a}_{1}(\sqrt{2})^{2}$=2,解得a1.再利用通项公式与求和公式即可得出.
解答 解:数列{an}满足an+1=$\sqrt{2}$an,可得:数列{an}是等比数列,公比为$\sqrt{2}$.
∵a3=2,∴${a}_{1}(\sqrt{2})^{2}$=2,解得a1=1.
∴a31=$1×(\sqrt{2})^{30}$=215,S30=$\frac{(\sqrt{2})^{30}-1}{\sqrt{2}-1}$=$(\sqrt{2}+1)({2}^{15}-1)$.
∴$(\sqrt{2}+1){a_{31}}-{S_{30}}$=$(\sqrt{2}+1)$215-$(\sqrt{2}+1)({2}^{15}-1)$=$\sqrt{2}$+1.
点评 本题考查了等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.一个几何体的三视图如图所示,则该几何体的体积等于( )


| A. | 72 | B. | 48 | C. | 24 | D. | 16 |
6.设集合A={x|-a<x<a},其中a>0,命题p:1∈A,命题q:2∈A,若p∨q为真命题,p∧q为假命题,则a的取值范围是( )
| A. | 0<a<1或a>2 | B. | 0<a<1或a≥2 | C. | 1<a≤2 | D. | 1≤a≤2 |
4.已知实数x,y满足$\left\{\begin{array}{l}{|x-y|≤1}\\{|x+y|≤3}\end{array}\right.$,则|3x+y|的最大值为( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
5.若($\sqrt{x}$+$\frac{2}{{x}^{2}}$)n展开式中只有第六项的二项式系数最大,则展开式中的常数项是( )
| A. | 90 | B. | 45 | C. | 120 | D. | 180 |
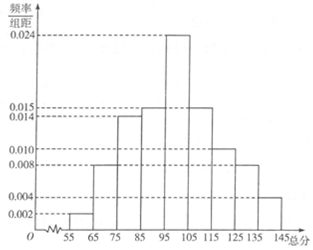 某省组织了一次高考模拟考试,该省教育部门抽取了1000名考生的数学考试成绩,并绘制成频率分布直方图如图所示.
某省组织了一次高考模拟考试,该省教育部门抽取了1000名考生的数学考试成绩,并绘制成频率分布直方图如图所示.