题目内容
13.已知命题p:已知两条直线l1:x+ay+1=0,l2:(a-2)x+3y+1=0,则a=-1是l1∥l2的充分不必要条件;命题q:“?x∈(0,1),x2-x<0”的否定为“?x0∈(0,1),x02-x0≥0”,则下列命题为真命题的是( )| A. | p∧(?q) | B. | (?p)∧q | C. | (?p)∧(?q) | D. | p∧q |
分析 对于命题p:由a(a-2)-3=0,解得a=3或a=-1.经过验证:即可判断出p的真假.对于命题q:利用全称命题与特称命题之间的关系即可判断出真假.再利用复合命题真假的判定方法即可得出答案.
解答 解:命题p:已知两条直线l1:x+ay+1=0,l2:(a-2)x+3y+1=0,由a(a-2)-3=0,解得a=3或a=-1.经过验证:a=3时两条直线重合,舍去.则a=-1是l1∥l2的充要条件;因此p是假命题.
命题q:“?x∈(0,1),x2-x<0”的否定为“?x0∈(0,1),x02-x0≥0”,是真命题.
则下列命题为真命题的是(¬p)∧q.
故选:B.
点评 本题考查了简易逻辑、直线相互平行的充要条件、方程的解法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
3.在△ABC中,$∠ACB=\frac{π}{6},BC=\sqrt{3},AC=4$,则AB等于( )
| A. | $\sqrt{7}$ | B. | 3 | C. | $\sqrt{11}$ | D. | $\sqrt{13}$ |
4.一个几何体的三视图如图所示,该几何体的表面积是$10+2\sqrt{5}$,则图中x的值为( )
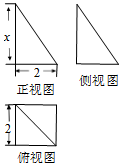

| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |
8.运行如图所示的程序,若输出y的值为1,则输入x的值为( )


| A. | 0 | B. | 0或-1 | C. | ±1 | D. | 1 |
5.一个几何体的三视图如图所示,则该几何体的体积等于( )


| A. | 72 | B. | 48 | C. | 24 | D. | 16 |