题目内容
20.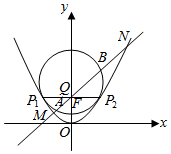 如图,抛物线C:x2=2py(p>0)的准线为y=-1,取过焦点F且平行于x轴的直线与抛物线交于不同的两点P1,P2,过P1,P2作圆心为Q的圆,使抛物线上其余点均在圆外,且∠P1QP2=90°.
如图,抛物线C:x2=2py(p>0)的准线为y=-1,取过焦点F且平行于x轴的直线与抛物线交于不同的两点P1,P2,过P1,P2作圆心为Q的圆,使抛物线上其余点均在圆外,且∠P1QP2=90°.(1)求抛物线C和圆Q的方程;
2)过点F作直线l与抛物线C和圆Q依次交于M,A,B,N,求|MN|•|AB|的最小值.
分析 (1)通过抛物线C:x2=2py(p>0)的准线为y=-1,求出p,得到抛物线方程,不妨设P1在左侧,求出P1的坐标,|P1F|=2,设圆Q的方程为:x2+(y-b)2=r2(b>1,r>0),通过P1Q⊥P2Q,求出b与r,得到圆的方程.
(2)直线l的斜率存在,设直线l的方程为:y=kx+1,求出圆心Q(0,3)到直线l的距离,推出|AB|,联立$\left\{{\begin{array}{l}{{x^2}=4y}\\{y=kx+1}\end{array}}\right.$
设M(x1,y1),N(x2,y2),由抛物线定义有:$|MN|={y_1}+{y_2}+2=4({k^2}+1)$,求出|MN|•|AB|的表达式,利用二次函数的性质求解最值即可.
解答 (本小题满分12分)
解:(1)因为抛物线C:x2=2py(p>0)的准线为y=-1,
所以$-\frac{p}{2}=-1$,解得p=2,所以抛物线C的方程为x2=4y. …(1分)
当y=1时,由x2=4y得:x=±2,不妨设P1在左侧,则P1(-2,1),|P1F|=2,…(2分)
由题意设圆Q的方程为:x2+(y-b)2=r2(b>1,r>0),
由∠P1QP2=90°且|P1Q|=|QP2|知:P1Q⊥P2Q,
∴△P1QP2是等腰直角三角形且∠QP1P2=45°,
∴|QF|=|P1F|=2,$|{P_1}Q|=\sqrt{|QF{|^2}+|{P_1}F{|^2}}=2\sqrt{2}$,则$b={3_{\;}},r=2\sqrt{2}$,…(4分)
∴圆Q的方程为:x2+(y-3)2=8. …(5分)
(2)由题意知直线l的斜率存在,设直线l的方程为:y=kx+1,
圆心Q(0,3)到直线l的距离为:$d=\frac{2}{{\sqrt{{k^2}+1}}}$,
∴$|AB|=2\sqrt{{r^2}-{d^2}}=4\sqrt{2-\frac{1}{{1+{k^2}}}}$. …(7分)
由$\left\{{\begin{array}{l}{{x^2}=4y}\\{y=kx+1}\end{array}}\right.$得:y2-(4k2+2)y+1=0,
设M(x1,y1),N(x2,y2),由抛物线定义有:$|MN|={y_1}+{y_2}+2=4({k^2}+1)$,…(9分)
∴$|MN|•|AB|=16({k^2}+1)•\sqrt{2-\frac{1}{{{k^2}+1}}}$,
设t=k2+1,则:t≥1且$|MN|•|AB|=16t•\sqrt{2-\frac{1}{t}}=16\sqrt{2{t^2}-t}=16\sqrt{2{{(t-\frac{1}{4})}^2}-\frac{1}{8}}$,…(11分)
∴当t=1即k=0时,|MN|•|AB|的最小值为16.…(12分)
点评 本题考查直线与抛物线的位置关系的应用,抛物线方程的求法,圆的方程的求法,考查计算能力.

 全优点练单元计划系列答案
全优点练单元计划系列答案 《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的体积为( )
《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的体积为( )| A. | 100πcm3 | B. | $\frac{500π}{3}c{m^3}$ | C. | 400πcm3 | D. | $\frac{4000π}{3}c{m^3}$ |

| A. | 0 | B. | 0或-1 | C. | ±1 | D. | 1 |
| A. | 664 | B. | 844 | C. | 968 | D. | 1204 |

| A. | 72 | B. | 48 | C. | 24 | D. | 16 |
| A. | -5 | B. | -1 | C. | 3 | D. | 4 |
| A. | -1+4i | B. | -1-4i | C. | 1+4i | D. | 1-4i |