题目内容
20.已知点N(2,0),圆M:(x+2)2+y2=36,点A是圆M上一个动点,线段AN的垂直平分线交AM于点P,则点P的轨迹方程是$\frac{x^2}{9}+\frac{y^2}{5}=1$.分析 由已知,得|PN|=|PA|,所以|PN|+|PM|=|PA|+|PM|=|MA|=6,又|MN|=4,4<6,根据椭圆的定义,点P的轨迹是M,N为焦点,以3为实轴长的椭圆,即可得出结论.
解答 解:由已知,得|PN|=|PA|,所以|PN|+|PM|=|PA|+|PM|=|MA|=6
又|MN|=4,4<6,根据椭圆的定义,点P的轨迹是M,N为焦点,以3为实轴长的椭圆,
所以2a=6,2c=4,所以$b=\sqrt{5}$,所以,点P的轨迹方程为:$\frac{x^2}{9}+\frac{y^2}{5}=1$.
故答案为:$\frac{x^2}{9}+\frac{y^2}{5}=1$.
点评 本题考查椭圆的方程与定义,考查学生的计算能力,正确运用椭圆的定义是关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
10.如图所示的等腰直角三角形表示一个水平放置的平面图形的直观图,则这个平面图形的面积是( ) 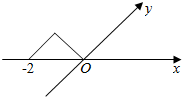

| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{{\sqrt{2}}}{2}$ |
5.已知抛物线y2=4x上的两点A,B满足|AB|=6,则弦AB中点到y轴的最小距离为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.函数$y=2sin(2x+\frac{π}{3})$的图象( )
| A. | 关于原点对称 | B. | 关于点($\frac{π}{6}$,0)对称 | ||
| C. | 关于y轴对称 | D. | 关于直线$x=\frac{π}{12}$对称 |
9.已知集合A={x|(x+1)(x-2)≤0},B={x|-2<x<2},则A∩B=( )
| A. | {x|-1≤x≤2} | B. | {x|-1≤x<2} | C. | {x|-1<x<2} | D. | {x|-2<x≤1} |
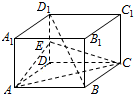 如图,正方体ABCD-A1B1C1D1的棱长为2,E为DD1的中点,
如图,正方体ABCD-A1B1C1D1的棱长为2,E为DD1的中点,