题目内容
8.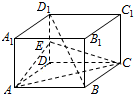 如图,正方体ABCD-A1B1C1D1的棱长为2,E为DD1的中点,
如图,正方体ABCD-A1B1C1D1的棱长为2,E为DD1的中点,(1)求证:BD1∥平面ACE;
(2)求△ACE的面积.
分析 (1)连结BD,令BD∩AC=F,连结EF,则EF∥BD1,由此能证明BD1∥平面ACE.
(2)由已知分别求出AF=$\sqrt{2}$,AE=$\sqrt{5}$,EF=$\sqrt{3}$,由此能求出△ACE的面积.
解答 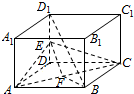 证明:(1)连结BD,令BD∩AC=F,连结EF.(2分)
证明:(1)连结BD,令BD∩AC=F,连结EF.(2分)
∵正方体ABCD-A1B1C1D1中,F是DB的中点,又E是DD1的中点,
∴EF∥BD1(4分)
又EF?平面ACE,BD1?平面ACE,
∴BD1∥平面ACE.(6分)
(2)在正方形ABCD中,AB=2,AC=2$\sqrt{2}$,∴AF=$\sqrt{2}$,(8分)
在直角△ADE中,AD=2,DE=1,∴AE=$\sqrt{5}$,
在Rt△EAF中,EF=$\sqrt{E{A^2}-A{F^2}}$=$\sqrt{5-2}$=$\sqrt{3}$,(10分)
∴${S_{△ACE}}=\frac{1}{2}×2\sqrt{2}×\sqrt{3}=\sqrt{6}$.(12分)
点评 本题考查线面平行的证明,考查三角形面积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
18.角θ的终边过点(3a-9,a+2),且sin2θ≤0,则a的范围是( )
| A. | (-2,3) | B. | [-2,3) | C. | (-2,3] | D. | [-2,3] |
19.命题“?a∈R,a2≥0”的否定为( )
| A. | ?a∈R,a2<0 | B. | ?a∈R,a2≥0 | C. | ?a∉R,a2≥0 | D. | ?a∈R,a2<0 |
16.p:|x-m|<1,q:x2-8x+12<0,且q是p的必要不充分条件,则m的取值范围是( )
| A. | 3<m<5 | B. | 3≤m≤5 | C. | m>5或m<3 | D. | m≥5或m≤3 |