题目内容
若等差数列{an}的首项为2，公差为d（d≠0），其前n项和Sn满足：对于任意的n∈N*，都有
是同一个非零常数，则d的值为（ ）
| S2n |
| Sn |
| A、4 | ||
| B、2 | ||
C、
| ||
D、
|
考点：等差数列的性质
专题：等差数列与等比数列
分析：利用特例法分别表示出S2和S4，根据已知建立等式求得d．
解答：
解：S1=a1=2，
S2=2+2+d=4+d，
S4=8+
=8+6d，
依题意知
=
，
∴
=
，求得d=4或d=0（舍），
故选：A．
S2=2+2+d=4+d，
S4=8+
| 4×3•d |
| 2 |
依题意知
| S2 |
| S1 |
| S4 |
| S2 |
∴
| 4+d |
| 2 |
| 8+6d |
| 4+d |
故选：A．
点评：本题主要考查了等差数列的性质．解题过程中采用了特例法，对于解决选择题是一个不错的方法．
练习册系列答案
相关题目
已知直线a、b，平面α、β，那么下列命题中正确的是（ ）
| A、若a⊥b，b⊥α，则a∥α |
| B、若a?α，b?β，a∥b，则α∥β |
| C、若a∥α，a⊥b，则b⊥α |
| D、若a∥α，a⊥β，则α⊥β |
若a＞0，b＞0，a+b=2，给出下列四个结论：①ab≤1②
+
≤
③a2+b2≥2④
+
≥2，其中所有正确结论的序号是（ ）
| a |
| b |
| 2 |
| 1 |
| a |
| 1 |
| b |
| A、①② | B、②③④ |
| C、③④ | D、①③④ |
函数y=loga（3x-2）（a＞0，a≠1）的图过定点A，则A点坐标是（ ）
A、（0，
| ||
B、（
| ||
| C、（1，0） | ||
| D、（0，1） |
设函数f（x）=
sin（ωx+φ+
）（0＜φ＜
）的最小正周期为π，且f（-x）=f（x），则（ ）
| 2 |
| π |
| 4 |
| π |
| 2 |
A、f（x）在（0，
| ||||
B、f（x）在（
| ||||
C、f（x）在（0，
| ||||
D、f（x）在（
|
光线从点A（-3，4）发出，经过x轴反射，再经过y轴反射，最后光线经过点B（-2，6），则经y轴反射的光线的方程为（ ）
| A、2x+y-2=0 |
| B、2x-y+2=0 |
| C、2x+y+2=0 |
| D、2x-y-2=0 |
下列函数f（x）中，在（0，+∞）上是减函数的是（ ）
A、f（x）=
| ||
| B、f（x）=x3 | ||
| C、f（x）=lnx | ||
| D、f（x）=2x |
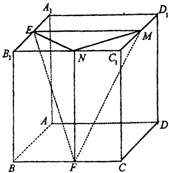如图，正方体ABCD-A1B1C1D1的棱长为1，E、F、M、N分别是A1B1、BC、C1D1、B1C1的中点．