题目内容
光线从点A(-3,4)发出,经过x轴反射,再经过y轴反射,最后光线经过点B(-2,6),则经y轴反射的光线的方程为( )
| A、2x+y-2=0 |
| B、2x-y+2=0 |
| C、2x+y+2=0 |
| D、2x-y-2=0 |
考点:与直线关于点、直线对称的直线方程
专题:直线与圆
分析:要求反射线所在直线的方程,我们根据已知条件所知的均为点的坐标,故可想办法求出反射线所在直线上两点,然后代入两点式即得直线方程,而根据反射的性质,我们不难得到反射光线所在直线上的两个点的坐标.
解答:
解:∵A(-3,4)关于x轴的对称点A1(-3,-4)在经x轴反射的光线上,
同样A1(-3,-4)关于y轴的对称点A2(3,-4)在经过射入y轴的反射线上,
kA2B=
=-2
故所求直线方程为y-6=-2(x+2),
即2x+y-2=0.
故选:A
同样A1(-3,-4)关于y轴的对称点A2(3,-4)在经过射入y轴的反射线上,
kA2B=
| 6+4 |
| -2-3 |
故所求直线方程为y-6=-2(x+2),
即2x+y-2=0.
故选:A
点评:本题主要考查直线方程的求法,属于基础题.

练习册系列答案
相关题目
A、B、C、D、E五人并排站成一排,如果A、B必须相邻且B在A的左边,那么不同的排法共有( )种.
| A、60 | B、36 | C、24 | D、48 |
若2,a,b,c,9成等差数列,则c-a的值为( )
| A、2.5 | B、3.5 |
| C、1.5 | D、3 |
 如图,过圆内接四边形ABCD的顶点C引圆的切线MN,AB为圆直径,若∠BCM=38°,则∠ABC=( )
如图,过圆内接四边形ABCD的顶点C引圆的切线MN,AB为圆直径,若∠BCM=38°,则∠ABC=( )| A、38° | B、52° |
| C、68° | D、42° |
已知集合A={x|x2-x-6<0},B={x|x2+2x-8>0},则A∩B=( )
| A、{x|-3<x<-2} |
| B、{x|2<x<3} |
| C、{x|-4<x<-2或2<x<3} |
| D、{x|3<x<4} |
已知a,b为非零实数,且a>b,则下列不等式成立的是( )
| A、a2b>ab2 | ||||
| B、a2>b2 | ||||
C、
| ||||
D、
|
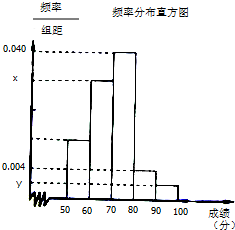 某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成的频率分布表和频率分布直方图(如图所示)解决下列问题:
某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成的频率分布表和频率分布直方图(如图所示)解决下列问题: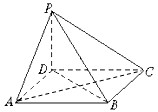 如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.
如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.