题目内容
已知向量
=(cosα,sinα),
=(cosβ,sinβ),0<α<β<π.
(1)若
⊥
,求|
-
|的值;
(2)设
=(0,1),若
+
=
,求α,β的值.
| a |
| b |
(1)若
| a |
| b |
| a |
| b |
(2)设
| c |
| a |
| b |
| c |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:(1)利用向量垂直得到cosαcosβ+sinαsinβ=0,要求|
-
|,先求其平方;
(2)利用向量相等,对应坐标相等得到α、β的三角函数等式,根据范围求角.
| a |
| b |
(2)利用向量相等,对应坐标相等得到α、β的三角函数等式,根据范围求角.
解答:
解:(1)由
⊥
,得cosαcosβ+sinαsinβ=0,所以|
-
|2=(cosα-cosβ)2+(sinα-sinβ)2=2,
所以|
-
|=
(2)由题意得:
又0<α<β<π,所以β=π-α
得sinα=sinβ=
,∴α=
,β=
.
| a |
| b |
| a |
| b |
所以|
| a |
| b |
| 2 |
(2)由题意得:
|
又0<α<β<π,所以β=π-α
得sinα=sinβ=
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
点评:本题考查了向量的数量积的公式,垂直的性质以及向量相等的意义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图为一个三棱柱的三视图,则该三棱柱的体积为( )


| A、1250 | B、2500 |
| C、3750 |
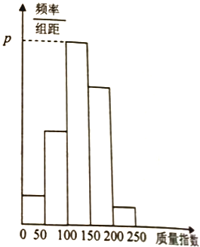 中华人民共和国关于《环境空气质量指数(AQI)技术规定(试行)》(HJ633-2012)中,关于空气质量指数划分如下表所示:
中华人民共和国关于《环境空气质量指数(AQI)技术规定(试行)》(HJ633-2012)中,关于空气质量指数划分如下表所示: