Question

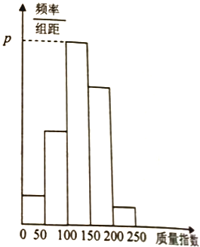中华人民共和国关于《环境空气质量指数（AQI）技术规定（试行）》（HJ633-2012）中，关于空气质量指数划分如下表所示：

AQI	0～50	51～100	101～150	151～200	201～300	＞300
级别	Ⅰ级	Ⅱ级	Ⅲ级	Ⅳ级	Ⅴ级	Ⅵ级
类别	优	良	轻度污染	中度污染	重度污染	严重污染

某市为了监测该市的空气质量指数，抽取一年中n天的数据进行分析，得到如下频率分布表及频率分布直方图：

分组	频数	频率
[0，50）	x	0.06
[50，100）	10	0.2
{100，150）	20	y
[150，200）	15	0.3
[200，250）	2	0.04
合计	n	1

（Ⅰ）求n、x、y和p的值；
（Ⅱ）利用样本估计总体的思想，估计该市一年中空气质量指数的平均数为多少？
（Ⅲ）该市政府计划通过对环境进行综合治理，使得今后Ⅲ的空气质量指数比上一年降低5%，问至少经过多少年后该市的空气质量可以达到优良水平？
（参考数据：0.95⁴≈0.815，0.95⁵≈0.774）

Answer 1

考点：频率分布直方图

专题：函数的性质及应用,概率与统计

分析：（Ⅰ）根据频率分布表，求出样本容量n以及x、y与p的值；
（Ⅱ）根据频率分布直方图，计算数据的平均数即可；
（Ⅲ）根据题意，列出不等式128×（1-0.05）^x≤100，求出x的值即可．

解答： 解：（Ⅰ）根据频率分布表，得；
数据在[50，100）内的频数是10，频率是0.2，
∴样本容量是n=

10

0.2

=50，
频数x=50×0.06=3，
频率y=

20

50

=0.4，
在频率分布直方图中，p是最高矩形的高度，
∴p=

0.4

50

=0.008；
（Ⅱ）根据频率分布直方图，得；
空气质量指数的平均数是

.

x

=25×0.06+75×0.2+125×0.4+175×0.3+225×0.04=128，
估计该市一年中空气质量指数的平均数为128；
（Ⅲ）根据题意，令128×（1-0.05）^x≤100，
即0.95^x≤0.781；
∵0.95⁵≈0.774＜0.781，
∴x≥5；
即至少经过5年后该市的空气质量可以达到优良水平．

点评：本题考查了频率分布的应用问题，也考查了函数模型的应用问题，是综合题目．