题目内容
已知向量
=(cos
x,sin
x),
=(cos
,-sin
),且x∈[0,
],则f(x)=
•
-4|
+
|的最小值为( )
| a |
| 3 |
| 2 |
| 3 |
| 2 |
| b |
| x |
| 2 |
| x |
| 2 |
| π |
| 2 |
| a |
| b |
| a |
| b |
| A、7 | ||
| B、-7 | ||
| C、6 | ||
D、
|
考点:平面向量数量积的运算
专题:计算题,三角函数的求值,平面向量及应用
分析:应用向量的数量积的坐标表示及模的平方等于向量的平方,结合两角和的余弦公式、二倍角公式,以及余弦函数的单调性,结合二次函数的值域,即可得到最小值.
解答:
解:由于向量
=(cos
x,sin
x),
=(cos
,-sin
),
则
•
=cos
cos
-sin
sin
=cos2x,|
|=|
|=1,
|
+
|=
=
=
=2cosx(x∈[0,
]),
则f(x)=
•
-4|
+
|=cos2x-8cosx=2cos2x-8cosx-1
=2(cosx-2)2-9,
由于cosx∈[0,1],则cosx=1,即x=0时,f(x)取得最小值,且为-7.
故选B.
| a |
| 3 |
| 2 |
| 3 |
| 2 |
| b |
| x |
| 2 |
| x |
| 2 |
则
| a |
| b |
| 3x |
| 2 |
| x |
| 2 |
| 3x |
| 2 |
| x |
| 2 |
| a |
| b |
|
| a |
| b |
|
| 1+1+2cos2x |
| 2×2cos2x |
=2cosx(x∈[0,
| π |
| 2 |
则f(x)=
| a |
| b |
| a |
| b |
=2(cosx-2)2-9,
由于cosx∈[0,1],则cosx=1,即x=0时,f(x)取得最小值,且为-7.
故选B.
点评:本题考查平面向量的数量积的坐标表示和性质,考查二倍角公式和两角和的余弦公式,考查余弦函数的单调性及应用,考查运算能力,属于中档题.

练习册系列答案
相关题目
若<
,
>=60°,|
|=4,(
+2
)•(
-3
)=-72,则|
|=( )
| a |
| b |
| b |
| a |
| b |
| a |
| b |
| a |
| A、2 | B、4 | C、6 | D、12 |
一个几何体的三视图如图所示,则这个几何体的表面积为( )
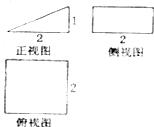

A、6+
| ||
B、6+2
| ||
C、8+
| ||
D、8+2
|
由
>
,
>
,
>
若a>b>0,m>0,则
与
的关系( )
| 7 |
| 10 |
| 5 |
| 8 |
| 9 |
| 11 |
| 8 |
| 10 |
| 21 |
| 25 |
| 15 |
| 19 |
| b+m |
| a+m |
| b |
| a |
| A、相等 | B、前者大 |
| C、后者大 | D、不确定 |
已知x、y的取值如表:从散点图分析,y与x线性相关,且回归方程为
=0.95x+a,则a=( )
 |
| y |
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
| A、2.6 | B、4 |
| C、4.5 | D、条件不足,无法求解 |