题目内容
集合A={x|x2+x-6＜0}，B={y|y=lg（x2+1）}，则A∩B等于（ ）
| A、（-3，2） |
| B、[0，3） |
| C、[0，+∞） |
| D、[0，2） |
考点：交集及其运算
专题：集合
分析：根据不等式求出对应集合的等价条件，利用集合的基本运算即可得到结论．
解答：
解：A={x|x2+x-6＜0}={x|-3＜x＜2}，
B={y|y=lg（x2+1）}={y|y≥0}，
则A∩B={x|0≤x＜2}=[0，2），
故选：D．
B={y|y=lg（x2+1）}={y|y≥0}，
则A∩B={x|0≤x＜2}=[0，2），
故选：D．
点评：本题主要考查集合的基本运算，利用不等式的解法求出集合对应元素是解决本题的关键，比较基础．
练习册系列答案
相关题目
如图所示，某地有一段网格状公路，小王开车从A处出发，选择最近的路线去往B处．因道路检修，虚线处公路无法行驶．若行至S路口处，小王会随机选择开向C，D两个路口之一，再选择避开S的最近路线继续行至B处，则小王共有（ ）种不同的行驶路线．| A、11 | B、20 | C、21 | D、23 |
命题p：?x∈R，sinx-cosx＜
，命题q：“a=1”是“直线l1：ax+2y-1=0与直线l2：x+（a+1）y+4=0平行”的充分条件，则下列命题中，真命题是（ ）
| 2 |
| A、（￢q）∨p |
| B、p∧q |
| C、（￢p）∧（￢q） |
| D、（￢p）∨（￢q） |
已知复数z满足z（1-i）=2i，其中i为虚数单位，则|z|=（ ）
| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |
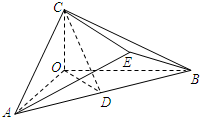如图，在三棱锥C-OAB中，CO⊥平面AOB，OA=OB=2OC=2，AB=2