题目内容
7.在△ABC中,角A、B、C所对的边分别为a、b、c,c-b=6,c+b-a=2,且O为此三角形的内心,则$\overrightarrow{AO}$•$\overrightarrow{CB}$=( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 设AD=x,BD=y,CE=z,则$\left\{\begin{array}{l}{x+y=c}\\{y+z=a}\\{z+x=b}\end{array}\right.$,解得x=$\frac{b+c-a}{2}$.由$\overrightarrow{CB}=\overrightarrow{AB}-\overrightarrow{AC}$,可得$\overrightarrow{AO}$•$\overrightarrow{CB}$=$\overrightarrow{AO}•\overrightarrow{AB}$-$\overrightarrow{AO}•\overrightarrow{AC}$=$|\overrightarrow{AD}|c$-$|\overrightarrow{AE}|$b=$|\overrightarrow{AD}|$(c-b)即可得出.
解答  解:设AD=x,BD=y,CE=z,
解:设AD=x,BD=y,CE=z,
则$\left\{\begin{array}{l}{x+y=c}\\{y+z=a}\\{z+x=b}\end{array}\right.$,解得x=$\frac{b+c-a}{2}$=1.
如图所示,
∵$\overrightarrow{CB}=\overrightarrow{AB}-\overrightarrow{AC}$,
∴$\overrightarrow{AO}$•$\overrightarrow{CB}$=$\overrightarrow{AO}•(\overrightarrow{AB}-\overrightarrow{AC})$=$\overrightarrow{AO}•\overrightarrow{AB}$-$\overrightarrow{AO}•\overrightarrow{AC}$
=$|\overrightarrow{AD}|c$-$|\overrightarrow{AE}|$b
=$|\overrightarrow{AD}|$(c-b)
=1×6
=6.
故选:C.
点评 本题考查了向量的三角形法则、数量积运算性质、三角形内切圆的性质,考查了推理能力与计算能力,属于中档题.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案| A. | {0} | B. | {2} | C. | {0,1,2,4,6} | D. | {0,2,3,5} |
| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | π | D. | $\frac{3π}{2}$ |
| A. | 27 | B. | 25 | C. | 23 | D. | 21 |
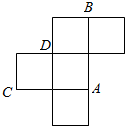 如图是一个无盖的正方体盒子展开后的平面图,A,B,C,D是展开图上的四点,则在正方体盒子中,直线AB与CD的位置关系是异面,∠ABC的值为60°.
如图是一个无盖的正方体盒子展开后的平面图,A,B,C,D是展开图上的四点,则在正方体盒子中,直线AB与CD的位置关系是异面,∠ABC的值为60°.