题目内容
12.已知向量$\overrightarrow{a}$=(sinx,2sinx),$\overrightarrow{b}$=(2cosx,-sinx),函数f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$.(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求函数y=f(x)在[-$\frac{π}{4}$,$\frac{3π}{8}$]上的值域.
分析 (Ⅰ)进行数量积的坐标运算可求出$\overrightarrow{a}•\overrightarrow{b}$,从而得出f(x)=$\sqrt{2}sin(2x+\frac{π}{4})-1$,从而得出f(x)的最小正周期为π;
(Ⅱ)可令$\frac{x}{2}+\frac{π}{4}$=t,并根据x的范围可以求出t$∈[-\frac{π}{4},π]$,从而可以求出sint在$[-\frac{π}{4},π]$的最大值和最小值,从而得出$\sqrt{2}sint-1$的最大、最小值,即得出y的范围,从而得出y=f(x)在[$-\frac{π}{4},\frac{3π}{8}$]上的值域.
解答 解:(Ⅰ)$\overrightarrow{a}•\overrightarrow{b}=2sinxcosx-2si{n}^{2}x$=$sin2x-1+cos2x=\sqrt{2}sin(2x+\frac{π}{4})-1$;
∴$f(x)=\sqrt{2}sin(2x+\frac{π}{4})-1$;
∴f(x)的最小正周期为π;
(Ⅱ)令2x+$\frac{π}{4}$=t;
∵$x∈[-\frac{π}{4},\frac{3π}{8}]$;
∴$t∈[-\frac{π}{4},π]$;
∴$t=\frac{π}{2}$时,sint取最大值1,∴$\sqrt{2}sint-1$取最大值$\sqrt{2}-1$;
t=$-\frac{π}{4}$时,sint取最小值$-\frac{\sqrt{2}}{2}$,∴$\sqrt{2}sint-1$取最小值-2;
∴y=f(x)在$[-\frac{π}{4},\frac{3π}{8}]$上的值域为$[-2,\sqrt{2}-1]$.
点评 考查数量积的坐标运算,二倍角的正余弦公式,以及两角和的正弦公式,计算y=Asin(ωx+φ)的最小正周期的公式:T=$\frac{2π}{|ω|}$,换元法求函数值域的方法,正弦函数在闭区间上的最值,要熟悉正弦函数的图象.

 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案| A. | $\frac{{\sqrt{3}{π^2}}}{4}-1$ | B. | $\frac{{3{π^2}}}{4}-1$ | C. | $\frac{{3{π^2}}}{2}-1$ | D. | $\frac{π^2}{2}-1$ |
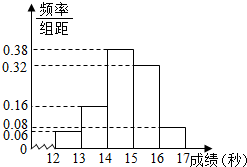 某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.
某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.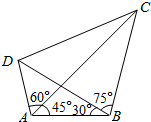 如图,在平面四边形ABCD中,AB=5$\sqrt{2}$,∠CBD=75°,∠ABD=30°,∠CAB=45°,∠CAD=60°.
如图,在平面四边形ABCD中,AB=5$\sqrt{2}$,∠CBD=75°,∠ABD=30°,∠CAB=45°,∠CAD=60°.