题目内容
19.已知函数$f(x)=\frac{1}{2}cos(ω\;x+\frac{π}{3})$,且f(x+3)-f(x)=0,则ω为( )| A. | $\frac{π}{2}$ | B. | $\frac{2π}{3}$ | C. | π | D. | $\frac{3π}{2}$ |
分析 由题意可得函数的周期为3=$\frac{2π}{ω}$,由此求得ω的值.
解答 解:由函数$f(x)=\frac{1}{2}cos(ω\;x+\frac{π}{3})$,且f(x+3)-f(x)=0,可得函数的周期为3=$\frac{2π}{ω}$,
求得ω=$\frac{2π}{3}$,
故选:B.
点评 本题主要考查函数的周期性的定义,余弦函数的周期性,属于基础题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
7.在△ABC中,角A、B、C所对的边分别为a、b、c,c-b=6,c+b-a=2,且O为此三角形的内心,则$\overrightarrow{AO}$•$\overrightarrow{CB}$=( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
11.直线y=kx+1与圆x2+y2=1的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相交或相切 | D. | 不能确定 |
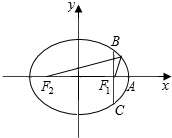 电影放映机上聚光灯泡的反射面,是由椭圆的一部分CAB(如图),绕着OA轴旋转而成的,如果把灯泡放在椭圆的一个焦点F1处,那么根据椭圆的光学性质,由F1发出光线,经反射面反射后,都集中在椭圆的另一个焦点F2处,因此,只要把影片放在F2处,就可以得到最强的光线,现已知|F1A|=1.5cm,|BC|=5.2cm,那么聚光灯泡F1与影片门F2之间应该距离多少cm.
电影放映机上聚光灯泡的反射面,是由椭圆的一部分CAB(如图),绕着OA轴旋转而成的,如果把灯泡放在椭圆的一个焦点F1处,那么根据椭圆的光学性质,由F1发出光线,经反射面反射后,都集中在椭圆的另一个焦点F2处,因此,只要把影片放在F2处,就可以得到最强的光线,现已知|F1A|=1.5cm,|BC|=5.2cm,那么聚光灯泡F1与影片门F2之间应该距离多少cm.