题目内容
16.已知数列{an}中,a1=1,an=an-1+$\frac{1}{2}$(n≥2),则数列{an}的前9项和等于( )| A. | 27 | B. | 25 | C. | 23 | D. | 21 |
分析 由已知得数列{an}是首项a1=1,公差an-an-1=$\frac{1}{2}$的等差数列,由此能求出数列{an}的前9项和.
解答 解:∵数列{an}中,a1=1,an=an-1+$\frac{1}{2}$(n≥2),
∴数列{an}是首项a1=1,公差an-an-1=$\frac{1}{2}$的等差数列,
∴数列{an}的前9项和:
${S}_{9}=9×1+\frac{9×8}{2}×\frac{1}{2}$=27.
故选:A.
点评 本题考查数列的前9项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
7.在△ABC中,角A、B、C所对的边分别为a、b、c,c-b=6,c+b-a=2,且O为此三角形的内心,则$\overrightarrow{AO}$•$\overrightarrow{CB}$=( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
11.直线y=kx+1与圆x2+y2=1的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相交或相切 | D. | 不能确定 |
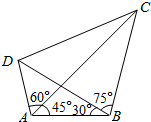 如图,在平面四边形ABCD中,AB=5$\sqrt{2}$,∠CBD=75°,∠ABD=30°,∠CAB=45°,∠CAD=60°.
如图,在平面四边形ABCD中,AB=5$\sqrt{2}$,∠CBD=75°,∠ABD=30°,∠CAB=45°,∠CAD=60°.