题目内容
15．已知点M是△ABC所在平面内的一点，且满足$7\overrightarrow{AM}=\overrightarrow{AB}+4\overrightarrow{AC}$，则△ABM与△ABC的面积之比为4：7．分析 根据条件$7\overrightarrow{AM}=\overrightarrow{AB}+4\overrightarrow{AC}$作出平行四边形，根据各线段的比例关系寻找对应三角形的面积比．
解答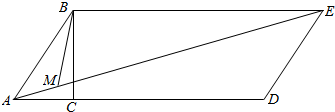 
解：连接AM，BM，延长AC至D使AD=4AC，延长AM至E使AE=7AM，连接BE，则四边形ABED是平行四边形．
∵AD=4AC，AE=7AM，
∴S△ABC=$\frac{1}{4}$S△ABD，S△AMB=$\frac{1}{7}$S△ABE，
∵S△ABD=S△ABE，∴S△ABM：S△ABC=$\frac{1}{7}$：$\frac{1}{4}$=4：7．
故答案为4：7．
点评 本题考查向量知识的运用，考查三角形面积的计算，解题的关键是确定三角形的面积，属于中档题．
练习册系列答案
相关题目
20．已知点P是函数y=sin（x+θ）图象与x轴的一个交点，A，B为P点右侧同一周期上的最大和最小值点，则$\overrightarrow{PA}•\overrightarrow{PB}$=（ ）
| A． | $\frac{{\sqrt{3}{π^2}}}{4}-1$ | B． | $\frac{{3{π^2}}}{4}-1$ | C． | $\frac{{3{π^2}}}{2}-1$ | D． | $\frac{π^2}{2}-1$ |