Question

已知如圆C₁：（x+5）²+y²=36，点C₂（5，0），动圆P过点C₂与C₁外切，求圆心P的轨迹方程．

Answer 1

考点：轨迹方程

专题：圆锥曲线的定义、性质与方程

分析：由已知得圆心P的轨迹是以C₁（-5，0），C₂（5，0）为焦点的双曲线，且双曲线的实轴为a=

1

2

||PC₁|-|PC₂||=

1

2

×6=3，由此能求出圆心P的轨迹方程．

解答： 解：由题意C₁（-5，0），||PC₁|-|PC₂||=6，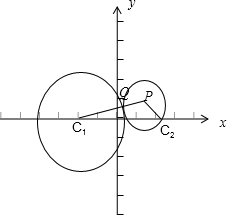
∴圆心P的轨迹是以C₁（-5，0），C₂（5，0）为焦点的双曲线，
且双曲线的实轴为a=

1

2

||PC₁|-|PC₂||=

1

2

×6=3，
∴设双曲线方程为

x2

a2

-

y2

b2

=1（a＞0，b＞0），
且a=3，c=5，
∴b²=25-9=16，
∴圆心P的轨迹方程为

x2

9

-

y2

16

=1．

点评：本题考查点的轨迹方程的求法，是中档题，解题时要认真审题，注意双曲线性质的合理运用．