题目内容
有一球体内切于正三棱锥,底面边长为a,高为h,求球半径r是多少?
考点:球的体积和表面积
专题:空间位置关系与距离
分析:如图所示,设球心为O点,底面中心为O1,球与侧面PBC相切与点E.由Rt△OPE∽Rt△DPO1,可得
=
,即可得出.
| OE |
| OP |
| O1D |
| PD |
解答:
解:如图所示,
设球心为O点,底面中心为O1,球与侧面PBC相切与点E.
则Rt△OPE∽Rt△DPO1,
∴
=
,
∴
=
,
解得r=
.

设球心为O点,底面中心为O1,球与侧面PBC相切与点E.
则Rt△OPE∽Rt△DPO1,
∴
| OE |
| OP |
| O1D |
| PD |
∴
| r |
| h-r |
| ||||||||
|
解得r=
| ah | ||
|
点评:本题考查了三棱锥的内切球的性质、相似三角形的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
若复数{kn}满足(1-i)z=i,则z在复平面内对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知集合A={0,1,2,3},B={1,3,4},则A∩B的真子集个数为( )
| A、2 | B、3 | C、4 | D、16 |
若异面直线l1,l2的方向向量分别是
=(0,-2,-1),
=(2,0,4),则异面直线l1与l2的夹角的余弦值等于( )
| a |
| b |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
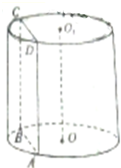 已知圆柱OO1的底面半径为2,高为4.
已知圆柱OO1的底面半径为2,高为4.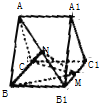 如图,在直三棱柱ABC-A1B1C1中,AA1=AC=1,BC=
如图,在直三棱柱ABC-A1B1C1中,AA1=AC=1,BC=