题目内容
若函数f（x）=3sin（ωx+φ）对任意实数x都有f（
+x）=f（
-x）恒成立，则f（
）的值为 ．
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
考点：正弦函数的对称性,三角函数的最值
专题：三角函数的图像与性质
分析：根据f（
+x）=f（
-x），求出对称轴．f（
）应该取函数的最值±3．
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
解答：
解：∵f（
+x）=f（
-x），∴对称轴x=
．
∴f（
）=±3．
故答案为：±3．
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
∴f（
| π |
| 3 |
故答案为：±3．
点评：本题考查了函数的对称性质以及在对称轴处取最值，属于基本知识的考查．
练习册系列答案
阅读快车系列答案
相关题目
集合A={x|x=2n，n∈Z}，B={y|y=4k，k∈Z}，则A与B的关系为（ ）
| A、A?B | B、A?B |
| C、A=B | D、A∈B |
在△ABC中，若有
=cos2
，则△ABC的形状是（ ）
| a+b |
| 2b |
| C |
| 2 |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、直角三角形或锐角三角形 |
设集合S={x|x≥2}，T={x|x≤5}，则S∩T=（ ）
| A、（2，5） |
| B、[2，5] |
| C、（-∞，5] |
| D、[2，+∞） |
已知集合A={0，1，2，3}，B={1，3，4}，则A∩B的真子集个数为（ ）
| A、2 | B、3 | C、4 | D、16 |
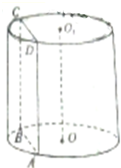已知圆柱OO1的底面半径为2，高为4．