Question

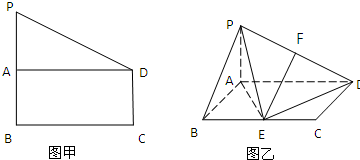
如图甲，在直角梯形PBCD中，PB∥CD，CD⊥BC，BC=PB=2CD，A是PB的中点，现沿AD把平面PAD折起，使得PA⊥AB（如图乙所示），E为BC边的中点．
（1）求证：PA⊥平面ABCD；
（2）设PD的中点为F，求证：EF∥平面PAB．

Answer 1

考点：直线与平面平行的判定,直线与平面垂直的判定

专题：空间位置关系与距离

分析：（1）由线线垂直得出线面垂直；（2）取PA的中点G，连BG，FG，得出四边形BEFG是平行四边形，得出线线平行，从而得出线面平行．

解答： 证明：（1）因为在图甲中PA⊥AD，翻折到图乙后不变，
又因为图乙中PA⊥AB，又AB∩AD=A，

所以PA⊥平面ABCD；
（2）取PA的中点G，连BG，FG，
在四边形BEFG中，FG∥AD，FG=

1

2

AD；
又BE∥AD，BE=

1

2

AD，
∴BE=FG，BE∥FG，
∴四边形BEFG是平行四边形，∴EF∥BG，
又EF?平面PAB，BG?平面PAB，
∴EF∥平面PAB．

点评：本题考查了线面垂直，线面平行的判断定理，考查数形结合思想，是一道基础题．