题目内容
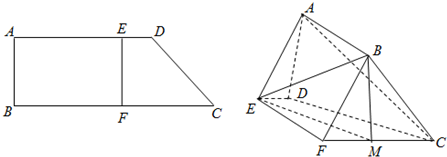
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,∠BCD=45°,E为AD上的点,EF⊥BC,垂足为F,沿EF将矩形ABFE折起,使二面角A-EF-C的大小为60°,连结AD,AC,BC.
(Ⅰ)若M为FC的中点,求证:AC∥平面BEM;
(Ⅱ)求直线CD与平面ABFE所成角的正弦值.
(Ⅰ)若M为FC的中点,求证:AC∥平面BEM;
(Ⅱ)求直线CD与平面ABFE所成角的正弦值.

考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)连结AF交BE于N,连结MN,由已知得MN∥AC,由此能证明AC∥平面BEM.
(Ⅱ)过E作EG∥DC交FC于G,则直线CD与平面ABFE所成角就是EG与平面ABFE所成角,由此能求出直线CD与平面ABFE所成角的正弦值.
(Ⅱ)过E作EG∥DC交FC于G,则直线CD与平面ABFE所成角就是EG与平面ABFE所成角,由此能求出直线CD与平面ABFE所成角的正弦值.
解答:
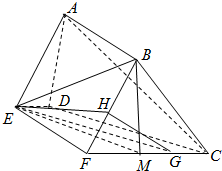 (Ⅰ)证明:连结AF交BE于N,连结MN,
(Ⅰ)证明:连结AF交BE于N,连结MN,
则N是AF的中点,又因为M为FC的中点,
则MN∥AC,
因为MN?平面BEM,AC?平面BEM,
所以AC∥平面BEM.
(Ⅱ)解:过E作EG∥DC交FC于G,
则直线CD与平面ABFE所成角就是EG与平面ABFE所成角,
过G作GH⊥BF于H,连结EH,
因为EF⊥BF,EF⊥CF,BF∩CF=F,
所以,∠BFC=60°,EF⊥平面BFC,
又GH?平面BFC,所以EF⊥GH,则GH⊥平面AEFB,
故∠GEH就是EG与平面ABFE所成角,
在直角△EFG中,EG=
FG,
在直角△HFG中,GH=
FG,即GH=
EG,
在直角△EGH中,sin∠GEH=
=
,
即直线CD与平面ABFE所成角的正弦值为
.
 (Ⅰ)证明:连结AF交BE于N,连结MN,
(Ⅰ)证明:连结AF交BE于N,连结MN,则N是AF的中点,又因为M为FC的中点,
则MN∥AC,
因为MN?平面BEM,AC?平面BEM,
所以AC∥平面BEM.
(Ⅱ)解:过E作EG∥DC交FC于G,
则直线CD与平面ABFE所成角就是EG与平面ABFE所成角,
过G作GH⊥BF于H,连结EH,
因为EF⊥BF,EF⊥CF,BF∩CF=F,
所以,∠BFC=60°,EF⊥平面BFC,
又GH?平面BFC,所以EF⊥GH,则GH⊥平面AEFB,
故∠GEH就是EG与平面ABFE所成角,
在直角△EFG中,EG=
| 2 |
在直角△HFG中,GH=
| ||
| 2 |
| ||
| 4 |
在直角△EGH中,sin∠GEH=
| GH |
| EG |
| ||
| 4 |
即直线CD与平面ABFE所成角的正弦值为
| ||
| 4 |
点评:本题考查直线与平面垂直的判定定理、平面与平面垂直的性质定理、勾股定理、二面角的求解等基础知识和空间向量的立体几何中的应用,意在考查方程思想、等价转化思想等数学思想方法和考生的空间想象能力、逻辑推理能力和运算求解能力.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
已知f(1)=1,f(x)=
(x=2,3,…),m∈N+,则f(2m)=( )
|
| A、2m+1 | |||||
B、
| |||||
C、
| |||||
| D、3m2+2m |
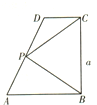 如图所示,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设
如图所示,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设