题目内容
已知函数f(x)=sinx•cos(x-
)+cos2x-
.
(1)求函数f(x)的单调递增区间和对称中心.
(2)在△ABC中,角A,B,C的对边分别为a,b,c,若f(A)=
,b+c=3,求a的最小值.
| π |
| 6 |
| 1 |
| 2 |
(1)求函数f(x)的单调递增区间和对称中心.
(2)在△ABC中,角A,B,C的对边分别为a,b,c,若f(A)=
| 1 |
| 2 |
考点:三角函数中的恒等变换应用,余弦定理
专题:三角函数的求值,三角函数的图像与性质,解三角形
分析:(1)首先通过三角函数的恒等变换把函数关系式变形成正弦型函数,进一步利用整体思想求出函数的单调区间和对称中心
(2)利用(1)的结论进一步计算出A的值,在利用余弦定理和基本不等式解出a的最小值.
(2)利用(1)的结论进一步计算出A的值,在利用余弦定理和基本不等式解出a的最小值.
解答:
解:(1)f(x)=sinx•cos(x-
)+cos2x-
=sinx(
cosx+
sinx)+cos2x-
=
sin2x+
=
sin(2x+
)+
令:-
+2kπ≤2x+
≤
+2kπ(k∈Z)
解得:kπ-
≤x≤kπ+
即函数的单调递增区间为:[kπ-
,kπ+
](k∈Z)
令:2x+
=kπ
解得:x=
-
(k∈Z)
即函数的对称中心为:(
-
,
)(k∈Z)
(2)利用函数f(x)=
sin(2x+
)+
则:f(A)=
sin(2A+
)+
=
则:sin(2A+
)=
由于:0<A<π
解得:A=
在△ABC中,角A,B,C的对边分别为a,b,c,b+c=3,
所以利用余弦定理得:
a2=b2+c2-2bccosA
=b2+c2-bc
=(b+c)2-3bc
因为:bc≤(
)2
则:(b+c)2-3bc≥(b+c)2-3(
)2=
进一步求得:a2≥
则:a≥
或a≤-
(舍去)
即:amin=
| π |
| 6 |
| 1 |
| 2 |
=sinx(
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| ||
| 4 |
| 1+cos2x |
| 4 |
=
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 4 |
令:-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解得:kπ-
| π |
| 3 |
| π |
| 6 |
即函数的单调递增区间为:[kπ-
| π |
| 3 |
| π |
| 6 |
令:2x+
| π |
| 6 |
解得:x=
| kπ |
| 2 |
| π |
| 12 |
即函数的对称中心为:(
| kπ |
| 2 |
| π |
| 12 |
| 1 |
| 4 |
(2)利用函数f(x)=
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 4 |
则:f(A)=
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 4 |
| 1 |
| 2 |
则:sin(2A+
| π |
| 6 |
| 1 |
| 2 |
由于:0<A<π
解得:A=
| π |
| 3 |
在△ABC中,角A,B,C的对边分别为a,b,c,b+c=3,
所以利用余弦定理得:
a2=b2+c2-2bccosA
=b2+c2-bc
=(b+c)2-3bc
因为:bc≤(
| b+c |
| 2 |
则:(b+c)2-3bc≥(b+c)2-3(
| b+c |
| 2 |
| 9 |
| 4 |
进一步求得:a2≥
| 9 |
| 4 |
则:a≥
| 3 |
| 2 |
| 3 |
| 2 |
即:amin=
| 3 |
| 2 |
点评:本题考查的知识要点:三角函数关系式的恒等变换,利用整体思想求正弦型函数的单调区间,及函数的对称中心,及利用余弦定理和基本不等式解三角形知识.属于基础题型.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
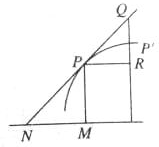 微积分的创立与求曲线的切线是密不可分的,历史上有很多关于曲线的研究.如图,设PN是曲线的切线,下面是两位数学家的说法:
微积分的创立与求曲线的切线是密不可分的,历史上有很多关于曲线的研究.如图,设PN是曲线的切线,下面是两位数学家的说法:①数学家Barrow认为:当弧PP′足够小(PP′→0)时,有
| PM |
| NM |
| P′R |
| PR |
②数学家Leibniz认为:令PR=dx,P′R=dy,当dx→0时,有PM→
| dy |
| dx |
则( )
| A、Barrow正确,Leibniz错误 |
| B、Leibniz正确,Barrow错误 |
| C、Barrow,Leibniz都正确 |
| D、Barrow,Leibniz都错误 |