题目内容
已知f(1)=1,f(x)=
(x=2,3,…),m∈N+,则f(2m)=( )
|
| A、2m+1 | |||||
B、
| |||||
C、
| |||||
| D、3m2+2m |
考点:分段函数的应用
专题:计算题,函数的性质及应用
分析:由f(1),求得f(2),即可排除A,B,再由假设C,D,推理论证,即可判断C错误,D正确.
解答:
解:由f(1)=1,可得f(2)=f(1)+4=1+4=5,可排除选项A和B;
又f(3)=f(2)+3=5+3=8,f(4)=f(3)+8=8+8=16,
若f(2m)=
,则f(2m)=f(2m-1)+4m,
即有f(2m-1)=4m2-3m+6-4m=4m2-7m+6(m≠1),
又f(2m-1)=f(2m-2)+2m-1=4(m-1)2-3(m-1)+6+2m-1=4m2-9m+12,
显然不成立,即选项C可排除;
若f(2m)=3m2+2m,则f(2m)=f(2m-1)+4m,
即有f(2m-1)=3m2-2m,
又f(2m-1)=f(2m-2)+2m-1=3(m-1)2+2(m-1)+2m-1=3m2-2m.
显然成立,则选项D正确.
故选:D.
又f(3)=f(2)+3=5+3=8,f(4)=f(3)+8=8+8=16,
若f(2m)=
|
即有f(2m-1)=4m2-3m+6-4m=4m2-7m+6(m≠1),
又f(2m-1)=f(2m-2)+2m-1=4(m-1)2-3(m-1)+6+2m-1=4m2-9m+12,
显然不成立,即选项C可排除;
若f(2m)=3m2+2m,则f(2m)=f(2m-1)+4m,
即有f(2m-1)=3m2-2m,
又f(2m-1)=f(2m-2)+2m-1=3(m-1)2+2(m-1)+2m-1=3m2-2m.
显然成立,则选项D正确.
故选:D.
点评:本题考查分段函数的运用,主要考查通过列举归纳数列的通项,运用排除法是解题的关键,属于中档题和易错题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,∠A=90°,AB=1,AC=2,设点P,Q满足
=λ
,
=(1-λ)
,λ∈R,
•
=-2.
(1)令
=
,
=
,用λ,
,
表示向量
和
;
(2)求λ的值.
| AP |
| AB |
| AQ |
| AC |
| BQ |
| CP |
(1)令
| AB |
| b |
| AC |
| c |
| b |
| c |
| BQ |
| CP |
(2)求λ的值.
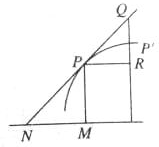 微积分的创立与求曲线的切线是密不可分的,历史上有很多关于曲线的研究.如图,设PN是曲线的切线,下面是两位数学家的说法:
微积分的创立与求曲线的切线是密不可分的,历史上有很多关于曲线的研究.如图,设PN是曲线的切线,下面是两位数学家的说法:①数学家Barrow认为:当弧PP′足够小(PP′→0)时,有
| PM |
| NM |
| P′R |
| PR |
②数学家Leibniz认为:令PR=dx,P′R=dy,当dx→0时,有PM→
| dy |
| dx |
则( )
| A、Barrow正确,Leibniz错误 |
| B、Leibniz正确,Barrow错误 |
| C、Barrow,Leibniz都正确 |
| D、Barrow,Leibniz都错误 |
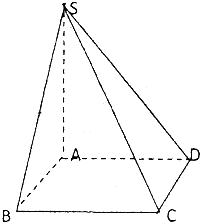 (文) 如图,四棱锥S-ABCD中,底面ABCD为正方形,SA⊥平面ABCD,AB=3,SA=4
(文) 如图,四棱锥S-ABCD中,底面ABCD为正方形,SA⊥平面ABCD,AB=3,SA=4