题目内容
三棱锥中有四条棱长为4,两条棱长为a,则a的取值范围为 .
考点:棱柱的结构特征
专题:空间位置关系与距离
分析:由题意确定当底面是边长为4的正三角形,三条侧棱长为4,a,a此时a取最大值;当构成三棱锥的两条对角线长为a,其他各边长为4,a有最小值,利用三角形的三边关系列出不等式,分别求出a的取值范围,再并在一起.
解答:
解:由题意得,三棱锥中有四条棱长为4,两条棱长为a,
有以下两种情况:如图,
①底面是边长为4的正三角形,三条侧棱长为4,a,a,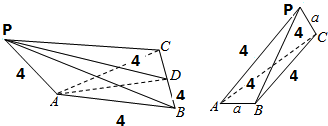 此时a可以取最大值,
此时a可以取最大值,
取BC的中点为D,连接AD、PD,则AD⊥BC,PD⊥BC
所以AD=2
,PD=
,
则
<4+2
,两边平方得a2<32+16
,
解得2<a<2
+2
,
②构成三棱锥的两条对角线长为a,其他各边长为4,如图所示,
此时a<2
,解得0<a<4
,
综上可得,a的取值范围是(0,2
+2
),
故答案为:(0,2
+2
).
有以下两种情况:如图,
①底面是边长为4的正三角形,三条侧棱长为4,a,a,
 此时a可以取最大值,
此时a可以取最大值,取BC的中点为D,连接AD、PD,则AD⊥BC,PD⊥BC
所以AD=2
| 3 |
| a2-4 |
则
| a2-4 |
| 3 |
| 3 |
解得2<a<2
| 6 |
| 2 |
②构成三棱锥的两条对角线长为a,其他各边长为4,如图所示,
此时a<2
42-(
|
| 2 |
综上可得,a的取值范围是(0,2
| 6 |
| 2 |
故答案为:(0,2
| 6 |
| 2 |
点评:本题考查的是空间想像能力,三角形的三边关系的应用,以及分类讨论思想、数形结合思想,正确画出几何体是解题的关键.

练习册系列答案
相关题目
 如图,已知抛物线C:y2=4x,过点A(1,2)作抛物线C的弦AP,AQ.设直线PQ过点T(5,-2),则以PQ为底边的等腰三角形APQ个数为 ( )
如图,已知抛物线C:y2=4x,过点A(1,2)作抛物线C的弦AP,AQ.设直线PQ过点T(5,-2),则以PQ为底边的等腰三角形APQ个数为 ( )