题目内容
设向量
=(2sin(x+
),-1),
=(2cosx,
),设函数f(x)=
•
(1)求函数f(x)的最小正周期
(2)若2f(x)-m+1=0在[0,
]内有两个相异的实根,求实数m的取值范围.
| a |
| π |
| 3 |
| b |
| 3 |
| a |
| b |
(1)求函数f(x)的最小正周期
(2)若2f(x)-m+1=0在[0,
| 3π |
| 4 |
考点:三角函数中的恒等变换应用,平面向量数量积的运算,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(1)由平面向量数量积的运算,三角函数中的恒等变换应用化简函数解析式可得f(x)=2sin(2x+
),由三角函数的周期性及其求法即可得解.
(2)由已知可转化为方程f(x)=
两个相异的实根,即y=f(x)图象与y=
图象有两个交点,结合函数图象,有
≤
<2或-2<
≤-1,即可解得m的取值范围.
| π |
| 3 |
(2)由已知可转化为方程f(x)=
| m-1 |
| 2 |
| m-1 |
| 2 |
| 3 |
| m-1 |
| 2 |
| m-1 |
| 2 |
解答:
解:(1)∵f(x)=
•
=4sin(x+
)cosx-
…1分
=2sinxcosx+2
cos2x-
…2分
=sin2x+
cos2x
=2sin(2x+
)…4分
∴T=π…6分
(2)2f(x)-m+1=0在[0,
]内有两个相异的实根,
即有方程:f(x)=
两个相异的实根,
即y=f(x)图象与y=
图象有两个交点,…8分
结合函数图象,当
≤
<2或-2<
≤-1,
即m∈[2
+1,5)∪(-3,-1]时原方程有两个相异的实根,
故m∈[2
+1,5)∪(-3,-1]…13分
| a |
| b |
| π |
| 3 |
| 3 |
=2sinxcosx+2
| 3 |
| 3 |
=sin2x+
| 3 |
=2sin(2x+
| π |
| 3 |
∴T=π…6分
(2)2f(x)-m+1=0在[0,
| 3π |
| 4 |
即有方程:f(x)=
| m-1 |
| 2 |
即y=f(x)图象与y=
| m-1 |
| 2 |
结合函数图象,当
| 3 |
| m-1 |
| 2 |
| m-1 |
| 2 |
即m∈[2
| 3 |
故m∈[2
| 3 |
点评:本题主要考查了平面向量数量积的运算,三角函数中的恒等变换应用,三角函数的周期性及其求法,考查了转化思想,属于中档题.

练习册系列答案
相关题目
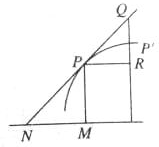 微积分的创立与求曲线的切线是密不可分的,历史上有很多关于曲线的研究.如图,设PN是曲线的切线,下面是两位数学家的说法:
微积分的创立与求曲线的切线是密不可分的,历史上有很多关于曲线的研究.如图,设PN是曲线的切线,下面是两位数学家的说法:①数学家Barrow认为:当弧PP′足够小(PP′→0)时,有
| PM |
| NM |
| P′R |
| PR |
②数学家Leibniz认为:令PR=dx,P′R=dy,当dx→0时,有PM→
| dy |
| dx |
则( )
| A、Barrow正确,Leibniz错误 |
| B、Leibniz正确,Barrow错误 |
| C、Barrow,Leibniz都正确 |
| D、Barrow,Leibniz都错误 |
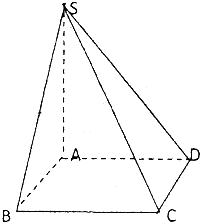 (文) 如图,四棱锥S-ABCD中,底面ABCD为正方形,SA⊥平面ABCD,AB=3,SA=4
(文) 如图,四棱锥S-ABCD中,底面ABCD为正方形,SA⊥平面ABCD,AB=3,SA=4
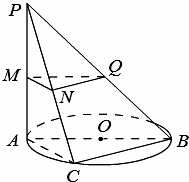 如图,⊙O在平面α内,AB是⊙O的直径,PA⊥平面α,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.
如图,⊙O在平面α内,AB是⊙O的直径,PA⊥平面α,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.