题目内容
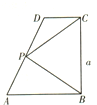 如图所示,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设
如图所示,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设| AP |
| AD |
| PB |
| PC |
①当a=2时,函数的值域为[1,4];
②?a∈(0,+∞),都有f(1)=1成立;
③?a∈(0,+∞),函数f(x)的最大值都等于4;
④若f(x)在(0,1)上单调减,则a∈(0,
| 2 |
其中所有正确结论的序号是
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:如图所示,建立直角坐标系.在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),可得B(0,0),A(-2,0),D(-1,a),C(0,a).
=x
,(0≤x≤1).可得
=
+
=(x-2,xa),
=
+
=(2-x,a-xa).y=f(x)=
•
=(a2+1)x2-(4+a2)x+4.,(0≤x≤1).
①当a=2时,y=f(x)=5x2-8x+4=5(x-
)2+
,利用二次函数的单调性即可得出;
②由y=f(x)=(a2+1)x2-(4+a2)x+4.可得:?a∈(0,+∞),都有f(1)=1成立;
③由y=f(x)=(a2+1)x2-(4+a2)x+4.可知:对称轴x0=
.当0<a≤
时,1<x0.当a>
时,0<x0<1,利用二次函数的单调性即可得出:
f(x)max=f(0).
④由③可得:f(x)在(0,1)上单调减,则a∈(0,
].
| AP |
| AD |
| BP |
| BA |
| AP |
| PC |
| PB |
| BC |
| PB |
| PC |
①当a=2时,y=f(x)=5x2-8x+4=5(x-
| 4 |
| 5 |
| 4 |
| 5 |
②由y=f(x)=(a2+1)x2-(4+a2)x+4.可得:?a∈(0,+∞),都有f(1)=1成立;
③由y=f(x)=(a2+1)x2-(4+a2)x+4.可知:对称轴x0=
| 4+a2 |
| 2(a2+1) |
| 2 |
| 2 |
f(x)max=f(0).
④由③可得:f(x)在(0,1)上单调减,则a∈(0,
| 2 |
解答:
解:如图所示,建立直角坐标系.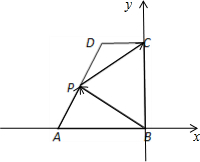
∵在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),
∴B(0,0),A(-2,0),D(-1,a),C(0,a).
∵
=x
,(0≤x≤1).
∴
=
+
=(-2,0)+x(1,a)=(x-2,xa),
=
+
=-(x-2,xa)+(0,a)=(2-x,a-xa).
∴y=f(x)=
•
=(2-x,-xa)•(2-x,a-xa)
=(2-x)2-ax(a-xa)
=(a2+1)x2-(4+a2)x+4.,(0≤x≤1).
①当a=2时,y=f(x)=5x2-8x+4=5(x-
)2+
,∵0≤x≤1,∴当x=
时,f(x)取得最小值
;又f(0)=4,f(1)=1,∴f(x)max=f(0)=4.综上可得:函数f(x)的值域为[
,1].因此①不正确.
②由y=f(x)=(a2+1)x2-(4+a2)x+4.可得:?a∈(0,+∞),都有f(1)=1成立,因此②正确;
③由y=f(x)=(a2+1)x2-(4+a2)x+4.可知:对称轴x0=
.当0<a≤
时,1<x0,∴函数f(x)在[0,1]单调递减,因此当x=0时,函数f(x)取得最大值4.当a>
时,0<x0<1,函数f(x)在[0,x0)单调递减,在(x0,1]上单调递增.又f(0)=4,f(1)=1,∴f(x)max=f(0)=4.因此③正确.
④由③可得:f(x)在(0,1)上单调减,则a∈(0,
],因此正确.
综上可知:只有②③④正确.
故答案为:②③④.

∵在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),
∴B(0,0),A(-2,0),D(-1,a),C(0,a).
∵
| AP |
| AD |
∴
| BP |
| BA |
| AP |
| PC |
| PB |
| BC |
∴y=f(x)=
| PB |
| PC |
=(2-x)2-ax(a-xa)
=(a2+1)x2-(4+a2)x+4.,(0≤x≤1).
①当a=2时,y=f(x)=5x2-8x+4=5(x-
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
②由y=f(x)=(a2+1)x2-(4+a2)x+4.可得:?a∈(0,+∞),都有f(1)=1成立,因此②正确;
③由y=f(x)=(a2+1)x2-(4+a2)x+4.可知:对称轴x0=
| 4+a2 |
| 2(a2+1) |
| 2 |
| 2 |
④由③可得:f(x)在(0,1)上单调减,则a∈(0,
| 2 |
综上可知:只有②③④正确.
故答案为:②③④.
点评:本题考查了向量数量积运算性质、二次函数的单调性,考查了分类讨论思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
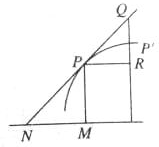 微积分的创立与求曲线的切线是密不可分的,历史上有很多关于曲线的研究.如图,设PN是曲线的切线,下面是两位数学家的说法:
微积分的创立与求曲线的切线是密不可分的,历史上有很多关于曲线的研究.如图,设PN是曲线的切线,下面是两位数学家的说法:①数学家Barrow认为:当弧PP′足够小(PP′→0)时,有
| PM |
| NM |
| P′R |
| PR |
②数学家Leibniz认为:令PR=dx,P′R=dy,当dx→0时,有PM→
| dy |
| dx |
则( )
| A、Barrow正确,Leibniz错误 |
| B、Leibniz正确,Barrow错误 |
| C、Barrow,Leibniz都正确 |
| D、Barrow,Leibniz都错误 |
 如图,已知四边形ABCD是正方形,PD⊥平面ABCD,CD=PD=2EA,PD∥EA,F,G,H分别为PB,BE,PC的中点.
如图,已知四边形ABCD是正方形,PD⊥平面ABCD,CD=PD=2EA,PD∥EA,F,G,H分别为PB,BE,PC的中点.
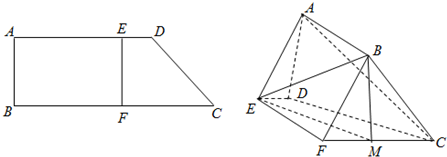
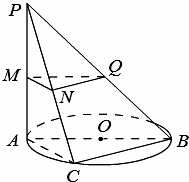 如图,⊙O在平面α内,AB是⊙O的直径,PA⊥平面α,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.
如图,⊙O在平面α内,AB是⊙O的直径,PA⊥平面α,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.