题目内容
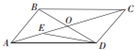如图所示，在平行四边形ABCD中，AC与BD交于点O，| AE |
| 1 |
| 4 |
| AC |
| AB |
| AD |
| DE |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：由
=
+
，
=
，
=
+
，即可得出．
| DE |
| DA |
| AE |
| AE |
| 1 |
| 4 |
| AC |
| AC |
| AB |
| AD |
解答：
解：∵
=
+
，
=
，
=
+
，
∴
=-
+
(
+
)
=-
+
=
-
．
故答案为：
-
．
| DE |
| DA |
| AE |
| AE |
| 1 |
| 4 |
| AC |
| AC |
| AB |
| AD |
∴
| DE |
| AD |
| 1 |
| 4 |
| AB |
| AD |
=-
| 3 |
| 4 |
| AD |
| 1 |
| 4 |
| AB |
=
| 1 |
| 4 |
| a |
| 3 |
| 4 |
| b |
故答案为：
| 1 |
| 4 |
| a |
| 3 |
| 4 |
| b |
点评：本题考查了向量的平行四边形法则、三角形法则、向量共线定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
若关于x的方程ax3-3x2+1=0正实数解有且仅有一个，则实数a的取值范围是（ ）
| A、{a|a≤0} |
| B、{a|a≤0或a=2} |
| C、{a|a≥0} |
| D、{a|a≥0或a=-2} |
若存在x使2•（x-a）＞1成立．则a的取值范围是（ ）
| A、（-∞．+∞） |
| B、（-2，+∞） |
| C、（0．+∞） |
| D、（-1，+∞） |
设k∈R，若关于x方程x2-kx+1=0的二根分别在区间（0，1）和（1，2）内，则k的取值范围为（ ）
| A、（-∞，-2）∪（2，+∞） | ||
B、（2，
| ||
| C、（1，3） | ||
D、（-∞，2）∪（
|