题目内容
若存在x使2•(x-a)>1成立.则a的取值范围是( )
| A、(-∞.+∞) |
| B、(-2,+∞) |
| C、(0.+∞) |
| D、(-1,+∞) |
考点:特称命题
专题:简易逻辑
分析:根据不等式,求出不等式的解,即可得到结论.
解答:
解:由2•(x-a)>1得x>
+a,
若存在x使2•(x-a)>1成立,
则a∈(-∞.+∞),
故选:A
| 1 |
| 2 |
若存在x使2•(x-a)>1成立,
则a∈(-∞.+∞),
故选:A
点评:本题主要考查特称命题的应用,根据不等式的关系是解决本题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
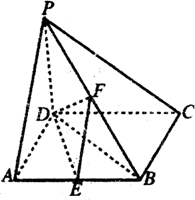 四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,E、F分别是AB、PB的中点.
四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,E、F分别是AB、PB的中点.(1)求证:PA⊥CD;
(2)求三棱锥B-DEF的体积;
(3)二面角E-DF-B的余弦值.
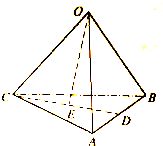 如图,在棱长均相等的四面体O-ABCD中,D为AB的中点,E为CD的中点,设
如图,在棱长均相等的四面体O-ABCD中,D为AB的中点,E为CD的中点,设| OA |
| a |
| OB |
| b |
| OC |
| c |
| OE |
| a |
| b |
| c |
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|
函数f(x)=(x+1)|log2x|-1的零点个数为( )
| A、1 | B、2 | C、3 | D、4 |
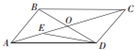 如图所示,在平行四边形ABCD中,AC与BD交于点O,
如图所示,在平行四边形ABCD中,AC与BD交于点O,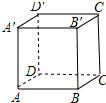 如图,正方体AC′的棱长为a.
如图,正方体AC′的棱长为a.