题目内容
若关于x的方程ax3-3x2+1=0正实数解有且仅有一个,则实数a的取值范围是( )
| A、{a|a≤0} |
| B、{a|a≤0或a=2} |
| C、{a|a≥0} |
| D、{a|a≥0或a=-2} |
考点:函数的零点
专题:函数的性质及应用
分析:有且仅有一个正数解”转化为“f(x)=ax3-3x2+1的图象与x正半轴有且仅有一个交点”,然后对函数f(x)进行求导,根据导数的正负判断函数的单调性并求出极小值,进而求解即可.
解答:
J解:设f(x)=ax3-3x2+1
∵f'(x)=3x(ax-2)
当a=0时,代入原方程知此时仅有一个正数解
;
当a>0时,令f'(x)>0,f'(x)<0,
得f(x)在(-∞,0)和(
,+∞)上单调递增,在(0,
)上单调递减,
f(0)=1,知若要满足条件只有x=
时f(x)取到极小值0.
x=
代入原方程得到a=2,正数解为x=1;
当a<0时,同理f(x)在(-∞,
)和(0,+∞)上单调递增,在(
,0)上单调递减,
f(0)=1>0,所以此时不存在满足条件的a;
故实数a的取值范围是(0,+∞);
故选C.
∵f'(x)=3x(ax-2)
当a=0时,代入原方程知此时仅有一个正数解
| ||
| 3 |
当a>0时,令f'(x)>0,f'(x)<0,
得f(x)在(-∞,0)和(
| 2 |
| a |
| 2 |
| a |
f(0)=1,知若要满足条件只有x=
| 2 |
| a |
x=
| 2 |
| a |
当a<0时,同理f(x)在(-∞,
| 2 |
| a |
| 2 |
| a |
f(0)=1>0,所以此时不存在满足条件的a;
故实数a的取值范围是(0,+∞);
故选C.
点评:本题主要考查根的存在性和区间的判定、根据导数的正负判断函数的单调性问题.考查基础知识的综合运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知S、A、B、C是球O表面上的点,SA⊥平面ABC,△ABC为等边三角形,SA=AB=1,则球O的表面积为( )
A、
| ||
B、
| ||
| C、π | ||
D、
|
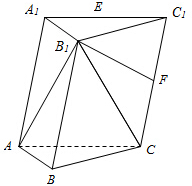 已知三棱柱ABC-A1B1C1中,△ABC是以AC为斜边的等腰直角三角形,且B1A=B1C=B1B=AC=2.
已知三棱柱ABC-A1B1C1中,△ABC是以AC为斜边的等腰直角三角形,且B1A=B1C=B1B=AC=2.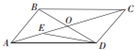 如图所示,在平行四边形ABCD中,AC与BD交于点O,
如图所示,在平行四边形ABCD中,AC与BD交于点O,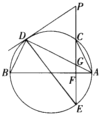 如图,P为圆外一点,PD为圆的切线,切点为D,AB为圆的一条直径,过点P作AB的垂线交圆于C、E两点(C、D两点在AB的同侧),垂足为F,连接AD交PE于点G.
如图,P为圆外一点,PD为圆的切线,切点为D,AB为圆的一条直径,过点P作AB的垂线交圆于C、E两点(C、D两点在AB的同侧),垂足为F,连接AD交PE于点G.