题目内容
已知以下4个命题:
①若p∨q为真命题,则p∧q为真命题;
②若p:?x∈R,x2-3x-2<0,则¬q:?x∈R,x2-3x-2≥0;
③设a,b∈R,则a>b是(a-1)|a|>(b-1)|b|成立的充分不必要条件;
④若关于实数x的不等式|1-2x|+|1+3x|<a|x|无解,则实数a的取值范围是(-∞,5].
其中正确命题的个数是( )
①若p∨q为真命题,则p∧q为真命题;
②若p:?x∈R,x2-3x-2<0,则¬q:?x∈R,x2-3x-2≥0;
③设a,b∈R,则a>b是(a-1)|a|>(b-1)|b|成立的充分不必要条件;
④若关于实数x的不等式|1-2x|+|1+3x|<a|x|无解,则实数a的取值范围是(-∞,5].
其中正确命题的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:阅读型,不等式的解法及应用,简易逻辑
分析:运用复合命题的真假和真值表,即可判断①;由全称性命题的否定为存在性命题,即可判断②;
由充分必要条件的定义和特殊值比如a=
,b=
,即可判断③;对x讨论,x=0.x≠0,运用分离参数,结合绝对值不等式的性质,求得最小值,即可判断④.
由充分必要条件的定义和特殊值比如a=
| 1 |
| 2 |
| 1 |
| 4 |
解答:
解:对于①,若p∨q为真命题,则p,q中至少有一个为真,则p∧q不一定为真命题,则①错误;
对于②,若p:?x∈R,x2-3x-2<0,则¬q:?x∈R,x2-3x-2≥0,则②正确;
对于③,设a,b∈R,当a>b,比如a=
,b=
,则(a-1)|a|=-
,(b-1)|b|=-
,
推出(a-1)|a|<(b-1)|b|,则③错误;
对于④,若关于实数x的不等式|1-2x|+|1+3x|<a|x|无解,当x=0,2<0无解,成立;
当x≠0时,即有a>|
-2|+|
+3|,由|
-2|+|
+3|≥|(
+3)-(
-2)|=5,
当a≤5时,不等式|1-2x|+|1+3x|<a|x|无解,则④正确.
综上可得,②④正确.
故选:B.
对于②,若p:?x∈R,x2-3x-2<0,则¬q:?x∈R,x2-3x-2≥0,则②正确;
对于③,设a,b∈R,当a>b,比如a=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 16 |
推出(a-1)|a|<(b-1)|b|,则③错误;
对于④,若关于实数x的不等式|1-2x|+|1+3x|<a|x|无解,当x=0,2<0无解,成立;
当x≠0时,即有a>|
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
当a≤5时,不等式|1-2x|+|1+3x|<a|x|无解,则④正确.
综上可得,②④正确.
故选:B.
点评:本题考查简易逻辑的基础知识,主要考查复合命题的真假和命题的否定及充分必要条件的判断,同时考查不等式的性质和绝对值不等式的基本性质,属于基础题和易错题.

练习册系列答案
相关题目
已知
,
是两个不共线的向量,向量
=
+sina•
(-
<a<
),
=2
-
,
=3
-
,若A,B,C三点共线,且函数f(x-a)=4cos(x-a)cos(x-2a),则f(x)在[-
,
]上的值域为( )
| e1 |
| e2 |
| PA |
| e1 |
| e2 |
| π |
| 2 |
| π |
| 2 |
| PB |
| e1 |
| e2 |
| PC |
| e1 |
| 5 |
| 2 |
| e2 |
| π |
| 4 |
| π |
| 6 |
A、[-2,
| ||||
B、[1-
| ||||
C、[-2
| ||||
D、[
|
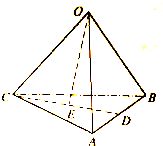 如图,在棱长均相等的四面体O-ABCD中,D为AB的中点,E为CD的中点,设
如图,在棱长均相等的四面体O-ABCD中,D为AB的中点,E为CD的中点,设| OA |
| a |
| OB |
| b |
| OC |
| c |
| OE |
| a |
| b |
| c |
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|
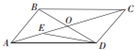 如图所示,在平行四边形ABCD中,AC与BD交于点O,
如图所示,在平行四边形ABCD中,AC与BD交于点O,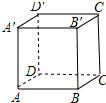 如图,正方体AC′的棱长为a.
如图,正方体AC′的棱长为a.