题目内容
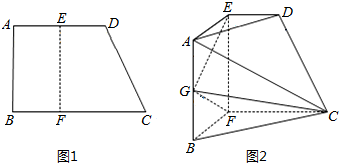
如图1,直角梯形ABCD中,∠A=∠B=90°,AD=AB=2,BC=3,E,F分别是AD,BC上的两点,且AE=BF=1,G为AB中点,将四边形ABCD沿EF折起到(图2)所示的位置,使得EG⊥GC,连接AD、BC、AC得(图2)所示六面体.
(Ⅰ)求证:EG⊥平面CFG;
(Ⅱ)求直线CD与平面CFG所成的角的正弦值.
(Ⅰ)求证:EG⊥平面CFG;
(Ⅱ)求直线CD与平面CFG所成的角的正弦值.

考点:直线与平面所成的角,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由已知得四边形ABFE为矩形,EF=AB=2,AG=BG=1,EG=GF=
,由勾股定理得EG⊥GF,由已知得EG⊥GC,由此能证明EG⊥平面CFG.
(Ⅱ)取CF中点H,连接EH,GH,由已知得四边形DCHE为平行四边形,HE与平面CFG所成的角即为CD与平面CFG所成的角,∠EHG为所求的角,由此能求出直线CD与平面CFG所成的角的正弦值.
| 2 |
(Ⅱ)取CF中点H,连接EH,GH,由已知得四边形DCHE为平行四边形,HE与平面CFG所成的角即为CD与平面CFG所成的角,∠EHG为所求的角,由此能求出直线CD与平面CFG所成的角的正弦值.
解答:
 (Ⅰ)证明:∵E,F分别是AD,BC上的两点,且AE=BF=1,
(Ⅰ)证明:∵E,F分别是AD,BC上的两点,且AE=BF=1,
∴四边形ABFE为矩形,∴EF=AB=2,
连结GF,GE,∵G为AB的中点,
∴AG=BG=1,解得EG=GF=
.
∵EF=2,∴EG2+FG2=EF2,
∴∠EGF=90°∴EG⊥GF.
又∵EG⊥GC,FG∩CG=G,GC⊆平面CFG,GF⊆平面CFG,
∴EG⊥平面CFG.
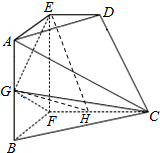
(Ⅱ)解:取CF中点H,连接EH,GH.则CH=
CF=1,
∵ED=1,∴CH=DF,∵CH∥DF,∴四边形DCHE为平行四边形,
故有CD∥HE,故HE与平面CFG所成的角即为CD与平面CFG所成的角,
∵EG⊥平面CFG,∴∠EHG为所求的角.
在Rt△EFH中,EH=
=
,
在Rt△EGF中,2EH2=EF2=4解得EG=
∴sin∠EHG=
=
,
∴直线CD与平面CFG所成的角的正弦值为
.
 (Ⅰ)证明:∵E,F分别是AD,BC上的两点,且AE=BF=1,
(Ⅰ)证明:∵E,F分别是AD,BC上的两点,且AE=BF=1,∴四边形ABFE为矩形,∴EF=AB=2,
连结GF,GE,∵G为AB的中点,
∴AG=BG=1,解得EG=GF=
| 2 |
∵EF=2,∴EG2+FG2=EF2,
∴∠EGF=90°∴EG⊥GF.
又∵EG⊥GC,FG∩CG=G,GC⊆平面CFG,GF⊆平面CFG,
∴EG⊥平面CFG.
(Ⅱ)解:取CF中点H,连接EH,GH.则CH=
| 1 |
| 2 |
∵ED=1,∴CH=DF,∵CH∥DF,∴四边形DCHE为平行四边形,
故有CD∥HE,故HE与平面CFG所成的角即为CD与平面CFG所成的角,
∵EG⊥平面CFG,∴∠EHG为所求的角.
在Rt△EFH中,EH=
| EF2+FH2 |
| 5 |
在Rt△EGF中,2EH2=EF2=4解得EG=
| 2 |
∴sin∠EHG=
| EG |
| EH |
| ||
| 5 |
∴直线CD与平面CFG所成的角的正弦值为
| ||
| 5 |
点评:本题考查直线与平面垂直的证明,考查直线与平面所成角的正弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
已知四面体OABC各棱长为1,D是棱OA的中点,则异面直线BD与AC所成角的余弦值( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知
,
是两个不共线的向量,向量
=
+sina•
(-
<a<
),
=2
-
,
=3
-
,若A,B,C三点共线,且函数f(x-a)=4cos(x-a)cos(x-2a),则f(x)在[-
,
]上的值域为( )
| e1 |
| e2 |
| PA |
| e1 |
| e2 |
| π |
| 2 |
| π |
| 2 |
| PB |
| e1 |
| e2 |
| PC |
| e1 |
| 5 |
| 2 |
| e2 |
| π |
| 4 |
| π |
| 6 |
A、[-2,
| ||||
B、[1-
| ||||
C、[-2
| ||||
D、[
|
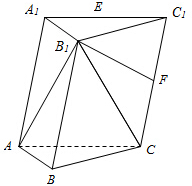 已知三棱柱ABC-A1B1C1中,△ABC是以AC为斜边的等腰直角三角形,且B1A=B1C=B1B=AC=2.
已知三棱柱ABC-A1B1C1中,△ABC是以AC为斜边的等腰直角三角形,且B1A=B1C=B1B=AC=2.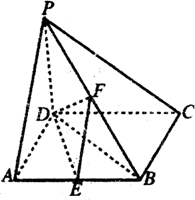 四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,E、F分别是AB、PB的中点.
四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC=2,E、F分别是AB、PB的中点. 如图所示,在平行四边形ABCD中,AC与BD交于点O,
如图所示,在平行四边形ABCD中,AC与BD交于点O,