题目内容
已知球的半径为r，其内接正四面体体积是 ．
考点：球内接多面体
专题：空间位置关系与距离
分析：正四面体扩展为正方体，它们的外接球是同一个球，正方体的对角线长就是球的直径，求出正方体的棱长即可求出正四面体的体积．
解答：
解：正四面体扩展为正方体，它们的外接球是同一个球，
正方体的对角线长就是球的直径，设正方体的棱长为a；对角线长为：
a，
则由
a=2r，得a=
r，∴正四面体的体积为a3-4×
a3=
a3=
r3．
故答案为：
r3．
正方体的对角线长就是球的直径，设正方体的棱长为a；对角线长为：
| 3 |
则由
| 3 |
2
| ||
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
8
| ||
| 27 |
故答案为：
8
| ||
| 27 |
点评：本题考查正四面体的外接球体积的求法，本题的突破口在正四面体转化为正方体，外接球是同一个球，考查计算能力，空间想象能力．
练习册系列答案
相关题目
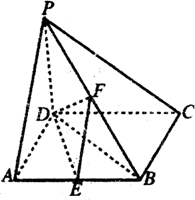四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC=2，E、F分别是AB、PB的中点．
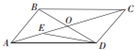如图所示，在平行四边形ABCD中，AC与BD交于点O，
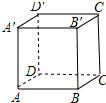如图，正方体AC′的棱长为a．