题目内容
9.在△ABC中,已知a=x,b=2,B=45°,如果三角形有两解,则x的取值范围是( )| A. | $2<x<2\sqrt{2}$ | B. | $x<2\sqrt{2}$ | C. | $\sqrt{2}<x<2$ | D. | 0<x<2 |
分析 由题意判断出三角形有两解时,A的范围,通过正弦定理及正弦函数的性质推出x的范围即可.
解答 解:由AC=b=2,要使三角形有两解,就是要使以C为圆心,半径为2的圆与BA有两个交点,
当A=90°时,圆与AB相切;
当A=45°时交于B点,也就是只有一解,
∴45°<A<135°,且A≠90°,即$\frac{\sqrt{2}}{2}$<sinA<1,
由正弦定理以及asinB=bsinA.可得:a=x=$\frac{bsinA}{sinB}$=2$\sqrt{2}$sinA,
∵2$\sqrt{2}$sinA∈(2,2$\sqrt{2}$).
∴x的取值范围是(2,2$\sqrt{2}$).
故选:A.
点评 此题考查了正弦定理,正弦函数的图象与性质,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键,属于中档题.

练习册系列答案
相关题目
14.如果集合A={x|mx2-4x+2=0}中只有一个元素,则实数m的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 0或2 |
18.某几何体的三视图如图所示,则该几何体的体积是( )


| A. | $\frac{4π}{3}$ | B. | $\frac{5π}{3}$ | C. | $2+\frac{2π}{3}$ | D. | $4+\frac{2π}{3}$ |
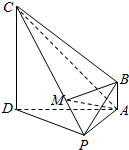 在四棱锥P-ABCD中,CD⊥平面PAD,AB∥CD,AD⊥PA,△ADC、△PAD均为等腰三角形,AD=4AB=4,M为线段CP上一点,且$\overrightarrow{PM}$=λ$\overrightarrow{PC}$(0≤λ≤1).
在四棱锥P-ABCD中,CD⊥平面PAD,AB∥CD,AD⊥PA,△ADC、△PAD均为等腰三角形,AD=4AB=4,M为线段CP上一点,且$\overrightarrow{PM}$=λ$\overrightarrow{PC}$(0≤λ≤1). 如图所示,在四棱锥A-BCDE中,AE⊥平面BCDE.△BCE是正三角形,BD和CE的交点恰好平分CE,又AE=BE=2,∠CDE=120°,AG=$\frac{\sqrt{2}}{2}$.
如图所示,在四棱锥A-BCDE中,AE⊥平面BCDE.△BCE是正三角形,BD和CE的交点恰好平分CE,又AE=BE=2,∠CDE=120°,AG=$\frac{\sqrt{2}}{2}$.