题目内容
1.在△ABC中,a=1,B=45°,S△ABC=2,则b=5.分析 由已知利用三角形面积公式可求c的值,根据余弦定理即可求b的值.
解答 解:∵在△ABC中,a=1,B=45°,S△ABC=2=$\frac{1}{2}$acsinB=$\frac{1}{2}×ac×\frac{\sqrt{2}}{2}$,可得:ac=4$\sqrt{2}$,
∴c=4$\sqrt{2}$,
∴b=$\sqrt{{a}^{2}+{c}^{2}-2accosB}$=$\sqrt{1+32-2×1×4\sqrt{2}×\frac{\sqrt{2}}{2}}$=5.
故答案为:5.
点评 本题主要考查了三角形面积公式,余弦定理在解三角形中的综合应用,属于基础题.

练习册系列答案
相关题目
11.已知命题p:?x0∈R,x02<x0,命题q:?x∈R,x2-x+1>0,则下列命题中为真命题的是( )
| A. | p∧q | B. | p∧¬q | C. | ¬p∧q | D. | ¬p∧¬q |
12.三棱锥A-BCD中,AB=AC=AD=2,∠BAD=90°,∠BAC=60°,则$\overrightarrow{AB}$•$\overrightarrow{CD}$等于( )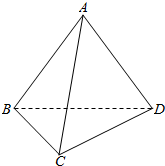

| A. | -2 | B. | 2 | C. | -2$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
9.在△ABC中,已知a=x,b=2,B=45°,如果三角形有两解,则x的取值范围是( )
| A. | $2<x<2\sqrt{2}$ | B. | $x<2\sqrt{2}$ | C. | $\sqrt{2}<x<2$ | D. | 0<x<2 |
6.已知a<b<0,则下列不等式成立的是( )
| A. | a2<b2 | B. | $\frac{a}{b}<1$ | C. | a<1-b | D. | $\frac{1}{a}<\frac{1}{b}$ |
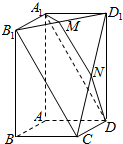 如图所示,多面体A1B1D1DCBA是长方体A1B1C1D-ABCD被平面B1CD1截去一个三棱锥后所得的几何体,M为B1D1的中点,过A1、D、M的平面交CD1于点N.
如图所示,多面体A1B1D1DCBA是长方体A1B1C1D-ABCD被平面B1CD1截去一个三棱锥后所得的几何体,M为B1D1的中点,过A1、D、M的平面交CD1于点N.